题目内容
18．若$|{b-1}|+\sqrt{a-4}=0$，且a，b是三角形的两边，则该三角形的第三边c的取值范是3＜c＜5．分析 先根据非负数的性质，求得a、b的值，再根据三角形的三边关系定理求得第三边c的取值范围．
解答 解：∵$|{b-1}|+\sqrt{a-4}=0$，
∴由非负数的性质可知，
a-4=0，b-1=0，解得a=4，b=1，
根据三角形的三边关系定理得，a-b＜c＜a+b，
即3＜c＜5，
故答案为：3＜c＜5．
点评 本题考查了非负数的性质，初中阶段所学的非负数有：算术平方根、偶次方，还考查了三角形的三边关系定理．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
名题训练系列答案
期末集结号系列答案
相关题目
8．若点（2，3）在反比例函数y=$\frac{k}{x}$（k≠0）的图象上，那么下列各点在图象上的是（ ）
| A． | （-2，3） | B． | （1，5） | C． | （1，6） | D． | （1，-6） |
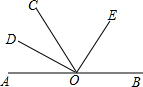如图所示，直线AB上有一点O，由O点引出一条射线OC，作∠AOC，∠BOC的平分线OD，OE．OD和OE垂直吗？若OC在转动，其他条件不变，上述条件成立吗？
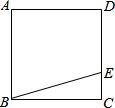如图，E为正方形ABCD的边CD上一点，将△BCE绕C点顺时针旋转90°后得到△DCF，则此时BE与DF的关系为相等、垂直．
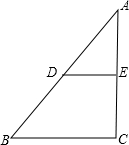如图，Rt△ABC中，D、E分别是边AB，AC的中点，DE=3，AB=10，则AC=8．
10．若一个角的余角是50°，则它的补角是（ ）
| A． | 140° | B． | 40° | C． | 130° | D． | 160° |