题目内容
13．
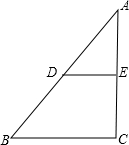如图，Rt△ABC中，D、E分别是边AB，AC的中点，DE=3，AB=10，则AC=8．
分析 先根据D、E分别是边AB，AC的中点得出DE是△ABC的中位线，根据中位线定理求出BC的长，再由勾股定理即可得出AC的长．
解答 解：∵D、E分别是边AB，AC的中点，DE=3，
∴DE是△ABC的中位线，
∴BC=2DE=6．
∵AB=10，
∴AC=$\sqrt{{AB}^{2}-{BC}^{2}}$=$\sqrt{{10}^{2}-{6}^{2}}$=8．
故答案为：8．
点评 本题考查的是三角形中位线定理，熟知三角形的中位线平行于第三边，并且等于第三边的一半是解答此题的关键．
练习册系列答案
名校课堂系列答案
相关题目
3．
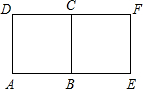如图，由正方形ABCD通过一次旋转得到正方形BCFE，其可能的旋转中心有（ ）个．
如图，由正方形ABCD通过一次旋转得到正方形BCFE，其可能的旋转中心有（ ）个．| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
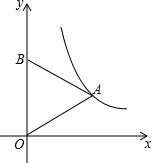如图，等边三角形OAB的顶点A在反比例函数y=$\frac{\sqrt{3}}{x}$的图象上，点B在y轴上，若将△OAB沿x轴正方向平移，当点B落在反比例函数的图象上时，点A的坐标为（$\frac{3\sqrt{3}}{2}$，1）．
1．
如图，∠1和∠2互补，∠3=130°，那么∠4的度数是（ ）
如图，∠1和∠2互补，∠3=130°，那么∠4的度数是（ ）| A． | 50° | B． | 60° | C． | 70° | D． | 80° |
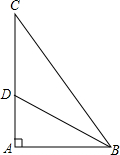如图所示，在Rt△ABC中，∠A=90°，BD平分∠ABC，交AC于点D，且AB=15，BD=17，则点D到BC的距离是8．