题目内容
6.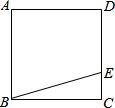 如图,E为正方形ABCD的边CD上一点,将△BCE绕C点顺时针旋转90°后得到△DCF,则此时BE与DF的关系为相等、垂直.
如图,E为正方形ABCD的边CD上一点,将△BCE绕C点顺时针旋转90°后得到△DCF,则此时BE与DF的关系为相等、垂直.
分析 如图,首先证明△BCE≌△DCF,得到BE=DF;其次证明BG⊥DF,即可解决问题.
解答  解:如图,延长BE,交DF于点G;
解:如图,延长BE,交DF于点G;
由旋转变换的性质知:△BCE≌△DCF,
∴BE=DF,∠CDF=∠GBF;
∵∠CDF+∠F=90°,
∴∠GBF+∠F=90°,
∴BG⊥DF,综上所述,
BE与DF的关系为:相等、垂直.
故答案为:相等、垂直.
点评 该题主要考查了旋转变换的性质、正方形的性质、全等三角形的性质等知识点的应用问题;应牢固掌握旋转变换的性质、正方形的性质等知识点.

练习册系列答案
相关题目
1. 如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
 如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )
如图,∠1和∠2互补,∠3=130°,那么∠4的度数是( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
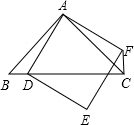 如图所示,四边形ADEF为正方形,△ABC为等腰直角三角形,D在BC边上,连接CF.
如图所示,四边形ADEF为正方形,△ABC为等腰直角三角形,D在BC边上,连接CF.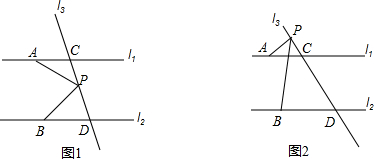
 如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论:
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,以点B为旋转中心,将线段BO逆时针旋转60°得到线段BO′,连接AO′.则下列结论: