题目内容
7.已知抛物线y=ax2经过点A(-2,4).(1)求该抛物线的函数关系式;
(2)判断点B(-$\sqrt{3}$,-3)是否在此抛物线上;
(3)若图象上有两点M(x1,y1)、N(x2,y2),其中|x1|<|x2|,则y1<y2(在横线上填“<”“=”或“>”).
分析 (1)根据待定系数法即可求得.
(2)把x=-$\sqrt{3}$代入y=x2求得y的值,比较点B的纵坐标即可判定.
(3)先根据二次函数的性质求出抛物线的对称轴为y轴,然后通过比较点M(x1,y1)和N(x2,y2)离直线y轴的远近得到y1与y2的大小.
解答 解:(1)∵抛物线y=ax2经过点A(-2,4).
∴4=(-2)2a,
∴a=1,
∴抛物线的函数关系式为(2)∵当x=-$\sqrt{3}$时,y=(-$\sqrt{3}$)2=3,
∴点B(-$\sqrt{3}$,-3)不在此抛物线上.
(3)∵抛物线y=x2的对称轴为y轴,图象上有两点M(x1,y1)、N(x2,y2),其中|x1|<|x2|,
∴M(x1,y1)比N(x2,y2)离y轴要近,
而抛物线开口向上,
∴y1<y2.
故答案为:<.
点评 本题考查了待定系数法求二次函数的解析式、二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
17.平面直角坐标系中,点P(3,5)位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
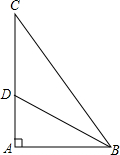 如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=15,BD=17,则点D到BC的距离是8.
如图所示,在Rt△ABC中,∠A=90°,BD平分∠ABC,交AC于点D,且AB=15,BD=17,则点D到BC的距离是8. 四边形ABCD的两条对角线相交于点O,AB∥CD,且AB=CD,S△AOB=5,则四边形ABCD的面积为20.
四边形ABCD的两条对角线相交于点O,AB∥CD,且AB=CD,S△AOB=5,则四边形ABCD的面积为20.