题目内容
用配方法解方程:2x2-4x+1=0的解是 .
考点:解一元二次方程-配方法
专题:
分析:移项、然后二次项系数化成1,配方、根据平方根的定义转化为两个一元一次方程,即可求解.
解答:解:移项,得:2x2-4x=-1,
二次项系数化成1得:x2-2x=-
,
配方,x2-2x+1=
,
即(x-1)2=
,则x-1=±
,
解得:x1=2+
,x2=2-
.
故答案是:x1=2+
,x2=2-
.
二次项系数化成1得:x2-2x=-
| 1 |
| 2 |
配方,x2-2x+1=
| 1 |
| 2 |
即(x-1)2=
| 1 |
| 2 |
| ||
| 2 |
解得:x1=2+
| ||
| 2 |
| ||
| 2 |
故答案是:x1=2+
| ||
| 2 |
| ||
| 2 |
点评:本题考查了配方法解方程,配方法的一般步骤:
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.
(1)把常数项移到等号的右边;
(2)把二次项的系数化为1;
(3)等式两边同时加上一次项系数一半的平方.
选择用配方法解一元二次方程时,最好使方程的二次项的系数为1,一次项的系数是2的倍数.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
 如图,直线y=-x+5与直线y=-
如图,直线y=-x+5与直线y=-| 1 |
| 2 |
| A、3 | B、3.5 | C、4 | D、4.5 |
 已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.
已知,如图,AB为⊙O的直径,E为⊙O外一点,EB,EC分别切⊙O于点B,C,求证:AC∥OE.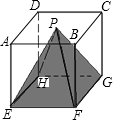 一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的,P为上底面ABCD的中心,如果挖去的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?
一个边长为5厘米的正方体,它是由125个边长为1厘米的小正方体组成的,P为上底面ABCD的中心,如果挖去的阴影部分为四棱锥,剩下的部分还包括多少个完整的棱长是1厘米的小正方体?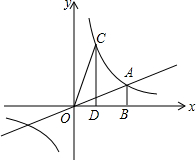 如图,直线y=
如图,直线y=