题目内容
3.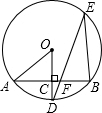 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.(1)若∠AOD=54°,求∠DEB的度数;
(2)若OC=3,OA=5,求弦AB的长.
分析 (1)欲求∠DEB,又已知一圆心角,可利用圆周角与圆心角的关系求解;
(2)利用垂径定理可以得到AC=BC=$\frac{1}{2}$AB=4,从而得到结论.
解答 解:(1)∵OD⊥AB,
∴$\widehat{AD}$=$\widehat{BD}$,
∴∠DEB=$\frac{1}{2}$∠AOD=$\frac{1}{2}$×54°=27°.
(2)∵OC=3,OA=5,
∴AC=4,
∵OD⊥AB,
∴弧AD=弧BD=$\frac{1}{2}$弧AB,
∴AC=BC=$\frac{1}{2}$AB=4,
∴AB=8.
点评 此题考查了圆周角与圆心角定理以及垂径定理,熟练掌握垂径定理得出AC=CB=4是解题关键.

练习册系列答案
相关题目
18.在一个不透明的盒子里装有3个黑球和1个白球,每个球除颜色外都相同,从中任意摸出2个球,下列条件中,不可能事件是( )
| A. | 摸出的2个球有一个是白球 | B. | 摸出的2个球都是黑球 | ||
| C. | 摸出的2个球有一个黑球 | D. | 摸出的2个球都是白球 |
8.如果点A(2,m)在抛物线y=x2上,将抛物线向右平移3个单位后,点A同时平移到点A′,那么A′坐标为( )
| A. | (2,1) | B. | (2,7) | C. | (5,4) | D. | (-1,4) |
12.在同一平面直角坐标系内,将函数y=x-3的图象向右平移2个单位,再向下平移1个单位得到的图象与x轴的交点坐标是( )
| A. | (-6,0) | B. | (2,0) | C. | (6,0) | D. | (-1,0) |
 如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.
如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE. 如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.
如图,数轴上点A、B、C所表示的数分别为a、b、c,点C是线段AB的中点,若原点O是线段AC上的任意一点,那么a+b-2c=0.