题目内容
13. 如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.
如图,DF⊥AC于F,BE⊥AC于E,AB=CD,DF=BE.求证:AF=CE.
分析 由HL证明Rt△ABE≌Rt△CDF,得出对应边相等AE=CF,由AE-EF=CF=EF,即可得出结论.
解答 证明:∵DF⊥AC,BE⊥AC,
∴∠CFD=∠AEB=90°,
在Rt△ABE和Rt△CDF中,$\left\{\begin{array}{l}{AB=CD}\\{BE=DF}\end{array}\right.$,
∴Rt△ABE≌Rt△CDF(HL),
∴AE=CF,
∴AE-EF=CF=EF,
∴AF=CE.
点评 本题考查了全等三角形的判定与性质;由HL证明三角形全等得出对应边相等是解决问题的关键.

练习册系列答案
相关题目
3.某企业2015年1月份生产产值为a万元,2月份比1月份减少了20%,3月份比2月份增加了25%,则3月份的生产产值是( )
| A. | (a-20%)(a+25%)万元 | B. | a(1-20%+25%)万元 | C. | (a-20%+25%)万元 | D. | a(1-20%)(1+25%)万元 |
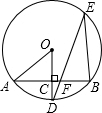 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.
如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,OD交⊙O于点D,点E在☉O上.