题目内容
12.“红星”中学准备为校“教学兴趣小组”购进甲、乙两种学习用具,已知5件甲种学习用具的进价与3件乙种学习用具的进价的和为231元,2件甲种学习用具的进价与3件乙种学习用具的进价的和为141元.(1)求每件甲种、乙种学习用具的进价分别是多少元?
(2)如果购进甲种学习用具有优惠,优惠方法是:购进甲种学习用具超过20件,超出部分可以享受7折优惠,若购进x(x>0)件甲种学习用具需要花费y元,请你求出y与x的函数关系式;
(3)在(2)的条件下,学校决定在甲、乙两种学习用具中选购其中一种,且数量超过20件,请你帮助学校判断购进哪种学习用具更省钱.
分析 (1)设每件甲种学习用具的进价是a元,每件乙种学习用具的进价是b元,根据花费钱数=单价×数量,结合两种不同购进方式可列出关于a、b的二元一次方程组,解方程组即可得出结论;
(2)结合优惠政策对x进行分段考虑,由花费钱数=单价×数量,可得出y关于x的函数关系式;
(3)找出购进乙种学习用具x件的花费,令乙种的花费<甲种的花费找出关于x的一元一次不等式,解出不等式即可得出结论.
解答 解(1)设每件甲种学习用具的进价是a元,每件乙种学习用具的进价是b元,
根据题意得:$\left\{\begin{array}{l}{5a+3b=231}\\{2a+3b=141}\end{array}\right.$,解得:$\left\{\begin{array}{l}{a=30}\\{b=27}\end{array}\right.$.
答:每件甲种学习用具的进价是30元,每件乙种学习用具的进价是27元.
(2)当0<x≤20时,y=30x;
当x>20时,y=20×30+0.7×30(x-20)=21x+180.
(3)购买x件乙种学习用具的花费为27x元,购买x件甲种学习用具的花费为(21x+180)元,
令27x<21x+180,解得:x<30.
即:当20<x<30时,购进乙种学习用具更省钱;当x=30时,两种学习用具的花费一样;当x>30时,购买甲种学习用具更省钱.
点评 本题考查了解二元一次方程组、一次函数的应用以及解一元一次不等式,解题的关键是:(1)根据已知列出关于a、b的二元一次方程组;(2)结合优惠政策分段寻找函数解析式;(3)令购买乙种的花费<购买甲种的花费找出此时的x的取值范围.本题属于中档题,难度不大,解决该类型题目时,把握住数量关系是关键.

练习册系列答案
 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案
相关题目
2.已知?ABCD的周长为32cm,AB=4cm,则BC长为( )
| A. | 4cm | B. | 12cm | C. | 24cm | D. | 28cm |
3.下列说法正确的是( )
| A. | 长度相等的弧是等弧 | |
| B. | 圆周角的度数一定等于圆心角度数的一半 | |
| C. | 面积相等的圆是等圆 | |
| D. | 劣弧一定比优弧短 |
20. 如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
 如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )
如图,把等腰直角三角板的直角顶点放在刻度尺的一边上,若∠1=60°,则∠2的度数为( )| A. | 30° | B. | 40° | C. | 50° | D. | 60° |
 如图,有一张长为8cm,宽为7cm的矩形纸片ABCD,现要剪下一个腰长为6cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm2.
如图,有一张长为8cm,宽为7cm的矩形纸片ABCD,现要剪下一个腰长为6cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm2.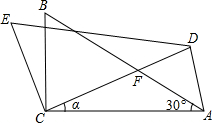 如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.
如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD. 我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达11公里处.
我市某出租车公司收费标准如图所示,如果小明只有19元钱,那么他乘此出租车最远能到达11公里处.