题目内容
17.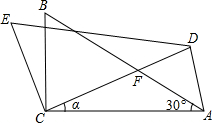 如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.
如图,在△ABC中,∠ACB=90°,∠BAC=90°,BC=2,将△ABC绕点C按逆时针方向旋转α角(0°<α<90°)得到△DEC,设CD交AB于点F.连接AD.(1)当α=30°时.
①求证:△BCF是等边三角形;
②求DF的长及△ADF的面积(结果保留根号);
(2)当旋转角α为何值时,△ADF是等腰三角形.
分析 (1)①由∠ACB=90°、∠BAC=30°、∠α=30°可得∠ABC=∠BCF=60°,得证;
②RT△ABC中求出AC=DC=2$\sqrt{3}$,由①知CF=BC=2,DF=DC-CF可得;作AP⊥DF于P,在RT△ACP中求得AP=$\frac{1}{2}$AC=$\sqrt{3}$,根据S△ADF=$\frac{1}{2}$DF•AP计算可得;
(2)根据旋转的性质可得AC=CD,根据等腰三角形的两底角相等求出∠ADF=∠DAC,再表示出∠DAF,根据三角形的一个外角等于与它不相邻的两个内角的和表示出∠AFD,然后分①∠ADF=∠DAF,②∠ADF=∠AFD,③∠DAF=∠AFD三种情况讨论求解.
解答 解:(1)①∵∠ACB=90°,∠BAC=30°,∠α=30°,
∴∠ABC=∠BCF=60°,
∴△BCF是等边三角形;
②RT△ABC中,∵BC=2,∠BAC=30°,
∴AB=2BC=4,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=2$\sqrt{3}$,
∵△DEC是由△ACB旋转得到,
∴DC=AC=$2\sqrt{3}$,
由①知,CF=BC=2,
∴DF=DC-CF=2$\sqrt{3}$-2;
作AP⊥DF于P,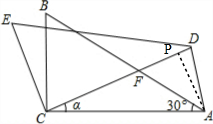
在RT△ACP中,∵∠α=30°,AC=2$\sqrt{3}$,
∴AP=$\frac{1}{2}$AC=$\sqrt{3}$,
∴S△ADF=$\frac{1}{2}$DF•AP=$\frac{1}{2}$×(2$\sqrt{3}$-2)×$\sqrt{3}$=3-$\sqrt{3}$;
(2)∵△ABC绕C点逆时针方向旋转得到△DEC,
∴AC=CD,
∴∠ADF=∠DAC=$\frac{1}{2}$(180°-α),
∴∠DAF=∠ADC-∠BAC=$\frac{1}{2}$(180°-α)-30°,
根据三角形的外角性质,∠AFD=∠BAC+∠DAC=30°+α,
△ADF是等腰三角形,分三种情况讨论,
①∠ADF=∠DAF时,$\frac{1}{2}$(180°-α)=$\frac{1}{2}$(180°-α)-30°,无解,
②∠ADF=∠AFD时,$\frac{1}{2}$(180°-α)=30°+α,解得α=40°,
③∠DAF=∠AFD时,$\frac{1}{2}$(180°-α)-30°=30°+α,解得α=20°,
综上所述,旋转角α度数为20°或40°.
点评 本题考查了旋转的性质、等边对等角的性质、直角三角形的有关性质、三角形的一个外角等于与它不相邻的两个内角的和的性质,难点在于要分情况讨论.

 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案| A. |  | B. |  | C. |  | D. |  |
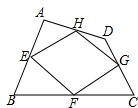 已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形).
已知:如图,四边形ABCD四条边上的中点分别为E、F、G、H,顺次连接EF、FG、GH、HE,得到四边形EFGH(即四边形ABCD的中点四边形). 在平面直角坐标系中,点A(2,3),B(5,-2),以原点O为位似中心,位似比为1:2,把△ABO缩小,则点B的对应点B′的坐标是($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).
在平面直角坐标系中,点A(2,3),B(5,-2),以原点O为位似中心,位似比为1:2,把△ABO缩小,则点B的对应点B′的坐标是($\frac{5}{2}$,-1)或(-$\frac{5}{2}$,1).