Question

7．如图，有一张长为8cm，宽为7cm的矩形纸片ABCD，现要剪下一个腰长为6cm的等腰三角形（要求：等腰三角形的一个顶点与矩形的一个顶点重合，其余的两个顶点在矩形的边上），则剪下的等腰三角形的面积为18或3$\sqrt{35}$或12$\sqrt{2}$cm²．

Answer 1

分析 因为等腰三角形腰的位置不明确，所以分三种情况进行讨论：
（1）△AEF为等腰直角三角形，直接利用面积公式求解即可；
（2）先利用勾股定理求出AE边上的高BF，再代入面积公式求解；
（3）先求出AE边上的高DF，再代入面积公式求解．

解答 解：分三种情况计算：
（1）当AE=AF=6时，如图：

∴S_△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$×6×6=18（cm²）；
（2）当AE=EF=6时，如图：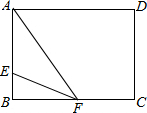

则BE=7-6=1，
BF=$\sqrt{E{F}^{2}-B{E}^{2}}$=$\sqrt{{6}^{2}-{1}^{2}}$=$\sqrt{35}$，
∴S_△AEF=$\frac{1}{2}$•AE•BF=$\frac{1}{2}$×6×$\sqrt{35}$=3$\sqrt{35}$（cm²）；
（3）当AE=EF=6时，如图：

则DE=8-6=2，
DF=$\sqrt{E{F}^{2}-D{E}^{2}}$=$\sqrt{{6}^{2}-{2}^{2}}$=4$\sqrt{2}$，
∴S_△AEF=$\frac{1}{2}$AE•DF=$\frac{1}{2}$×6×4$\sqrt{2}$=12$\sqrt{2}$（cm²）；
故答案为：18或3$\sqrt{35}$或12$\sqrt{2}$．

点评 本题主要考查了勾股定理的运用，矩形的性质，三角形的面积，要根据三角形的腰长的不确定分情况讨论，有一定的难度．