题目内容
13.已知二次函数y=x2-2ax+6,当-2≤x≤2时,y≥a,则实数a的取值范围是( )| A. | -2≤a≤2 | B. | $-\frac{10}{3}≤a≤-2$ | C. | $-\frac{10}{3}≤a≤2$ | D. | 0≤a≤2 |
分析 利用配方法可得出抛物线的对称轴以及函数的最小值,分a<-2、a>2和-2≤a≤2三种情况,根据二次函数的性质结合y≥a,即可得出关于a的一元一次不等式(二元一次不等式),解之即可得出a的取值范围,再综合三种情况下的a的取值范围即可.
解答 解:∵y=x2-2ax+6=(x-a)2-a2+6,
∴函数图象开口向上,对称轴为x=a,最小值为-a2+6.
①当a<-2时,在-2≤x≤2上y随x的增大而增大,
∵y≥a,
∴(-2)2-2a×(-2)+6=10+4a≥a,
解得:-$\frac{10}{3}$≤a.
∵a<-2,
∴-$\frac{10}{3}$≤a<-2;
②当a>2时,在-2≤x≤2上y随x的增大而减小,
∵y≥a,
∴22-2a×2+6=10-4a≥a,
解得:a≤2.
∵a>2,
∴无解;
③当-2≤a≤2时,函数在x=a处取最小值-a2+6.
∵y≥a,
∴-a2+6≥a,
解得:-3≤a≤2.
∵-2≤a≤2,
∴-2≤a≤2.
综上可得:-$\frac{10}{3}$≤a≤2.
故选C.
点评 本题考查了二次函数的性质以及二次函数的三种形式,分a<-2、a>2和-2≤a≤2三种情况,找出关于a的一元一次不等式(二元一次不等式)是解题的关键.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
1.我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )
| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | 1 |
5. 某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
请你根据以上信息,解答下列问题:
(1)a=0.5,b=8,c=6,并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.
 某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:
某校七年级有400名学生,在一次生物测验后,为了解本次测验的成绩情况,从中随机取了部分学生的成绩进行统计,并绘制了如下图表:| 等级 | 分数 | 频数 | 频率 |
| A | 90≤x≤100 | 6 | 0.15 |
| B | 80≤x<90 | 20 | a |
| C | 70≤x<80 | b | 0.2 |
| D | 60≤x<70 | c | 0.15 |
| 合计 | 1 |
(1)a=0.5,b=8,c=6,并补全条形统计图;
(2)请你估计该校七年级共有多少名学生本次成绩不低于80分;
(3)现从样本中的A等和D等学生中各随机选取一名同学组成互助学习小组,则直接写出两名同学恰好是一名男生和一名女生的概率.
3.红星中学课外兴趣活动小组对某水稻品种的稻穗谷粒数目进行调查,从试验田中随机抽取了30株,得到的数据如下(单位:颗):
(1)对抽取的30株水稻稻穗谷粒数进行统计分析,请补全下表中空格,并完善直方图:

如图所示的扇形统计图中,扇形A对应的圆心角为72度,扇形B对应的圆心角为36度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
| 182 | 195 | 201 | 179 | 208 | 204 | 186 | 192 | 210 | 204 |
| 175 | 193 | 200 | 203 | 188 | 197 | 212 | 207 | 185 | 206 |
| 188 | 186 | 198 | 202 | 221 | 199 | 219 | 208 | 187 | 224 |
| 谷粒颗数 | 175≤x<185 | 185≤x<195 | 195≤x<205 | 205≤x<215 | 215≤x<225 |
| 频数 | 3 | 8 | 10 | 6 | 3 |
| 对应扇形 图中区域 | B | D | E | A | C |

如图所示的扇形统计图中,扇形A对应的圆心角为72度,扇形B对应的圆心角为36度;
(2)该试验田中大约有3000株水稻,据此估计,其中稻穗谷粒数大于或等于205颗的水稻有多少株?
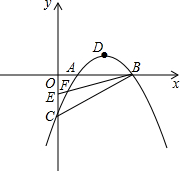 已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC
已知抛物线y=ax2+bx+c与x轴交于A(1,0),B(3,0),与y轴交于C(0,-2),顶点为D,点E的坐标为(0,-1),该抛物线于BE交于另一点F,连接BC 完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.
完全平方式(a+b)2=a2+2ab+b2中,等式右边各项系数依次是1,2,1,那么,(a+b)3,(a+b)4,…(a+b)n展开后的各项系数有什么规律呢?11世纪中叶,我国数学家贾宪给出了直到(a+b)6的系数表(如图),请观察系数表,请写出(a+b)7展开后从左向右第三项的系数21.