题目内容
1.我们知道:等腰三角形、平行四边形、菱形、双曲线、抛物线.这些都是我们在初中学习阶段学过的几何图形或函数的图象,那么从它们之中随机抽取两个,得到的都是中心对称图形的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{3}{10}$ | C. | $\frac{1}{2}$ | D. | 1 |
分析 将等腰三角形、平行四边形、菱形、双曲线、抛物线分别记作A,B,C,D,E,再列表,根据所得的结果进行计算即可.
解答 解:五种图形中,属于中心对称图形的有:平行四边形、菱形、双曲线,
将等腰三角形、平行四边形、菱形、双曲线、抛物线分别记作A,B,C,D,E,
列表可得:
总共有20种等可能的情况,其中抽取的两个都是中心对称图形的有6种,
∴P(抽取的两个都是中心对称图形)=$\frac{6}{20}$=$\frac{3}{10}$,
故选:B.
点评 本题主要考查了中心对称图形以及概率的计算,解题时注意:当有两个元素时,可用树形图列举,也可以列表列举.列表的目的在于不重不漏地列举出所有可能的结果求出n,再从中选出符合事件A或B的结果数目m,求出概率.

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案 ABC考王全优卷系列答案
ABC考王全优卷系列答案
相关题目
9.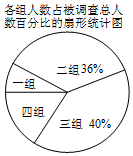 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
被调查同学每周课外阅读时间统计表.
(1)本次随机调查学生共有50名,表格中a的值为20,在扇形统计图中第一组对应的圆心角的度数是28.8度;
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
 “读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:
“读书”是一种诗意的生存状态,一种幸福的生活方式,一种温暖的生命体验.随着央视《朗读者》的播出,某校带领全体师生走进阅读,洗涤心灵.某班同学为了解该校学生每周课外阅读的时间,在全校随机调查了部分学生,对这部分同学的课外阅读时间x(小时)进行了整理,并制作了如下不完全的统计表格和扇形统计图:被调查同学每周课外阅读时间统计表.
| 组号 | 分组 | 频数 |
| 一 | 0≤x<2 | 4 |
| 二 | 2≤x<4 | 18 |
| 三 | 4≤x<6 | a |
| 四 | 6≤x<8 | 8 |
(2)学校为进一步推动好此次阅读活动,决定举办一次“诵读生命”活动,准备在第一组四名同学中随机选取两名同学参加“诵读生命”活动,以督促他们课外阅读.已知四名同学中有一名男生,三名女生,请求出选取的两名同学中恰好一名是男生,一名是女生的概率.
13.已知二次函数y=x2-2ax+6,当-2≤x≤2时,y≥a,则实数a的取值范围是( )
| A. | -2≤a≤2 | B. | $-\frac{10}{3}≤a≤-2$ | C. | $-\frac{10}{3}≤a≤2$ | D. | 0≤a≤2 |
11.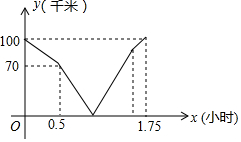 在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
 在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )
在同一条道路上,甲车从A地到B地,乙车从B地到A地,乙先出发,图中的折线段表示甲、乙两车之间的距离y(千米)与行驶时间x(小时)的函数关系的图象,下列说法错误的是( )| A. | 乙先出发的时间为0.5小时 | B. | 甲的速度是80千米/小时 | ||
| C. | 甲出发0.5小时后两车相遇 | D. | 甲到B地比乙到A地早$\frac{1}{12}$小时 |
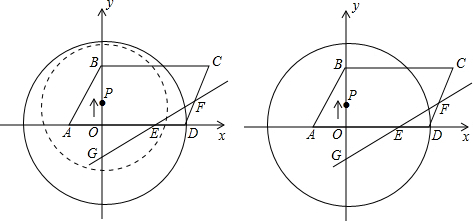
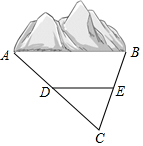 某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE的长为1200m,则隧道AB的长度为2400米.
某地需要开辟一条隧道,隧道AB的长度无法直接测量.如图所示,在地面上取一点C,使点C均可直接到达A,B两点,测量找到AC和BC的中点D,E,测得DE的长为1200m,则隧道AB的长度为2400米. 如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.
如图,已知一次函数y=kx-4k+5的图象与反比例函数y=$\frac{3}{x}$(x>0)的图象相交于点A(p,q).当一次函数y的值随x的值增大而增大时,p的取值范围是$\frac{3}{5}$<p<4.