题目内容
 如图,直线y=x-1与反比例函数y=
如图,直线y=x-1与反比例函数y=| k |
| x |
(1)求反比例函数的解析式;
(2)若点P(n,-1)是反比例函数图象上一点,过点P作PE⊥x轴于点E,延长EP交直线AB于点F,求△CEF的面积;
(3)若B(2,1),当x为何值时,一次函数的值大于反比例函数的值.
考点:反比例函数综合题
专题:
分析:(1)将点A的坐标代入直线解析式求出m的值,再将点A的坐标代入反比例函数解析式可求出k的值,继而得出反比例函数关系式;
(2)将点P的纵坐标代入反比例函数解析式可求出点P的横坐标,将点P的横坐标和点F的横坐标相等,将点F的横坐标代入直线解析式可求出点F的纵坐标,将点的坐标转换为线段的长度后,即可计算△CEF的面积.
(3)找到一次函数在反比例函数图象上的x的取值范围.
(2)将点P的纵坐标代入反比例函数解析式可求出点P的横坐标,将点P的横坐标和点F的横坐标相等,将点F的横坐标代入直线解析式可求出点F的纵坐标,将点的坐标转换为线段的长度后,即可计算△CEF的面积.
(3)找到一次函数在反比例函数图象上的x的取值范围.
解答:解:(1)将点A的坐标代入y=x-1,可得:m=-1-1=-2,
将点A(-1,-2)代入反比例函数y=
,可得:k=-1×(-2)=2,
故反比例函数解析式为:y=
.
(2)将点P的纵坐标y=-1,代入反比例函数关系式可得:x=-2,
将点F的横坐标x=-2代入直线解析式可得:y=-3,
故可得EF=3,CE=OE+OC=2+1=3,
故可得S△CEF=
CE×EF=
.
(3)结合图形可得:当x>2或-1<x<0时一次函数的值大于反比例函数的值.
将点A(-1,-2)代入反比例函数y=
| k |
| x |
故反比例函数解析式为:y=
| 2 |
| x |
(2)将点P的纵坐标y=-1,代入反比例函数关系式可得:x=-2,
将点F的横坐标x=-2代入直线解析式可得:y=-3,
故可得EF=3,CE=OE+OC=2+1=3,
故可得S△CEF=
| 1 |
| 2 |
| 9 |
| 2 |
(3)结合图形可得:当x>2或-1<x<0时一次函数的值大于反比例函数的值.
点评:本题考查了反比例函数的综合,解答本题的关键是确定点A的坐标,要求同学们能结合图象及直角坐标系,将点的坐标转化为线段的长度.

练习册系列答案
相关题目
 如图,在△ABC中,AD、CE分别为BC、AB边上高,且BE:BC=1:2,∠DAC=45°,DE=3,求△ABC三边的长.
如图,在△ABC中,AD、CE分别为BC、AB边上高,且BE:BC=1:2,∠DAC=45°,DE=3,求△ABC三边的长.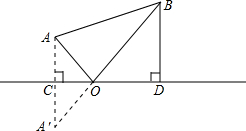 如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.
如图,A、B两个村子在河CD的同侧,AB2=13km,A、B两村子到河的距离分别为AC=1km,BD=3km.现在要在河边CD上建一水厂,向A、B村输送自来水,铺设水管的工程费为每千米3000元,请你在CD上选择水厂的位置O,使铺设水管费用的最省,并求出铺设水管的总费用W.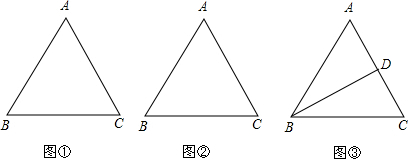
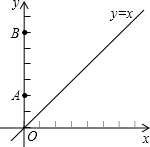 在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的坐标是多少?
在平面直角坐标系xOy中,A(0,2),B(0,6),动点C在直线y=x上.若以A、B、C三点为顶点的三角形是等腰三角形,则点C的坐标是多少? 如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,CD=1,则AC=
如图,在△ABC中,∠C=90°,AC=BC,AD是∠BAC的平分线,CD=1,则AC=