题目内容
 已知直线y=
已知直线y=| 3 |
| 4 |
| 1 |
| 4 |
(1)求抛物线的解析式和点C的坐标;
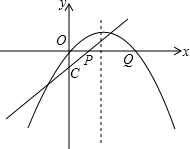
(2)把(1)中的抛物线向右平移2个单位,再向上平移m个单位(m>0),抛物线与x轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,求m的值;
(3)如图,把抛物线向右平移2个单位,再向上平移n个单位(n>0),抛物线与x轴交于P、Q两点,过C、P、Q三点的圆的面积是否存在最小值?若存在,请求出这个最小值和此时n的值;若不存在,请说明理由.
考点:二次函数综合题
专题:
分析:(1)把点A的坐标,代入抛物线y=ax2即可得出抛物线的解析式为y=-
x2,把点A的坐标代入直线y=
x+b,可得到直线的解析式为y=
x-1,再运用直线与y轴交于点C.即可求出点C的坐标,
(2)由已知先求出新的抛物线的解析式,由抛物线与x轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,得出∠CPQ=90°,即P点正好在原点上,把P的坐标代入y=-
(x-2)2+m,即可得出m的值.
(3)存在,由抛物线平移后其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,其面积为最小值为S=πr2=4π,由已知得出新的抛物线的解析式为y=-
(x-2)2+n,设P(t,0)再由E(2,-1),PE=2,列出关于t的方程(t-2)2+1=4,解得t的值,再代入y=-
(x-2)2+n,即可得到时n的值.
| 1 |
| 4 |
| 3 |
| 4 |
| 3 |
| 4 |
(2)由已知先求出新的抛物线的解析式,由抛物线与x轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,得出∠CPQ=90°,即P点正好在原点上,把P的坐标代入y=-
| 1 |
| 4 |
(3)存在,由抛物线平移后其对称轴是x=2.由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,则符合条件的圆是以E为圆心,EC长为半径的圆,其面积为最小值为S=πr2=4π,由已知得出新的抛物线的解析式为y=-
| 1 |
| 4 |
| 1 |
| 4 |
解答:解:(1)∵把点A(1,-
),代入抛物线y=ax2得a=-
∴抛物线的解析式为y=-
x2,
∵把点A(1,-
),代入直线y=
x+b,解得b=-1,
∴直线的解析式为y=
x-1,
∵直线与y轴交于点C.
∴C(0,-1).
(2)∵把(1)中的抛物线向右平移2个单位,再向上平移m个单位(m>0),
∴新的抛物线的解析式为y=-
(x-2)2+m,
∵抛物线与x轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,
∴∠CPQ=90°,
∴P点正好在原点上,
把P(0,0)代入y=-
(x-2)2+m,得m=1.
(3)存在最小值,如图,
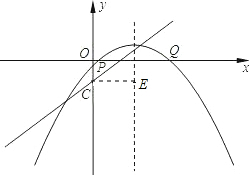
理由如下:
抛物线平移后其对称轴是x=2.
由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EC长为半径的圆,
其面积为最小值为S=πr2=4π,
∵抛物线向右平移2个单位,再向上平移n个单位(n>0),
∴新的抛物线的解析式为y=-
(x-2)2+n,
设P(t,0)
∵E(2,-1),PE=2,
∴(t-2)2+1=4,解得t=2-
代入y=-
(x-2)2+n,得n=
.
| 1 |
| 4 |
| 1 |
| 4 |
∴抛物线的解析式为y=-
| 1 |
| 4 |
∵把点A(1,-
| 1 |
| 4 |
| 3 |
| 4 |
∴直线的解析式为y=
| 3 |
| 4 |
∵直线与y轴交于点C.
∴C(0,-1).
(2)∵把(1)中的抛物线向右平移2个单位,再向上平移m个单位(m>0),
∴新的抛物线的解析式为y=-
| 1 |
| 4 |
∵抛物线与x轴交于P、Q两点,过C、P、Q三点的圆恰好以CQ为直径,
∴∠CPQ=90°,
∴P点正好在原点上,
把P(0,0)代入y=-
| 1 |
| 4 |
(3)存在最小值,如图,

理由如下:
抛物线平移后其对称轴是x=2.
由于过P、Q的圆的圆心必在对称轴上,要使圆的面积最小,则圆的半径要最小,
即点C到圆心的距离要最短,过C作CE垂直抛物线的对称轴,垂足为E,
则符合条件的圆是以E为圆心,EC长为半径的圆,
其面积为最小值为S=πr2=4π,
∵抛物线向右平移2个单位,再向上平移n个单位(n>0),
∴新的抛物线的解析式为y=-
| 1 |
| 4 |
设P(t,0)
∵E(2,-1),PE=2,
∴(t-2)2+1=4,解得t=2-
| 3 |
代入y=-
| 1 |
| 4 |
| 3 |
| 4 |
点评:本题主要考查了二次函数与方程、几何知识的综合应用,解题的关键是将函数问题转化为方程问题,善于利用几何图形的有关性质、定理和二次函数的知识求解.

练习册系列答案
相关题目
 如图所示,C是⊙O上一点,O是圆心,若∠AOB=80°,则∠ACB=( )
如图所示,C是⊙O上一点,O是圆心,若∠AOB=80°,则∠ACB=( )| A、20° | B、30° |
| C、40° | D、50° |


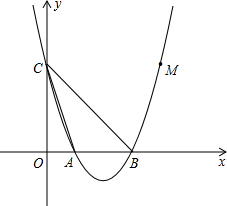 如图,已知抛物线y=a(x-1)(x-3)与x轴从左至右分别交于A、B两点,与y轴交于点C,且抛物线过点M(4,3),连接AC、BC.
如图,已知抛物线y=a(x-1)(x-3)与x轴从左至右分别交于A、B两点,与y轴交于点C,且抛物线过点M(4,3),连接AC、BC.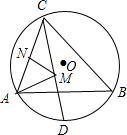 如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值.
如图,△ABC内接于半径为2的⊙O,其中∠ABC=45°,∠ACB=60°,CD平分∠ACB交⊙O于D,点M、N分别是线段CD、AC上的动点,求MA+MN的最小值.
 已知:如图,圆O1与圆O2都经过点A、B,过点A引直线CD、MN,分别交两圆于D、M和C、N,DM、NC的延长线交于P,连结BM、BN.求证:∠P+∠MBN=180°.
已知:如图,圆O1与圆O2都经过点A、B,过点A引直线CD、MN,分别交两圆于D、M和C、N,DM、NC的延长线交于P,连结BM、BN.求证:∠P+∠MBN=180°.