题目内容
如图,已知抛物线y=ax2+bx+c经过A(-3,0),B(1,0),C(0,3)三点,其顶点为D,对称轴是直线l,l与x轴交于点H.
(1)求该抛物线的解析式;
(2)如图(1),PQ是该抛物线对称轴l上的动线段,且PQ=1,直接写出PC+QB的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.求S与m的函数关系式,并求出S的最大值;
(4)若点M为抛物线上异于F的一个动点,在第(3)问△ADF的面积S取最大值的情况下,若S△MAD=3S△ADF,请直接写出M点坐标.

(1)求该抛物线的解析式;
(2)如图(1),PQ是该抛物线对称轴l上的动线段,且PQ=1,直接写出PC+QB的最小值;
(3)如图(2),若E是线段AD上的一个动点( E与A、D不重合),过E点作平行于y轴的直线交抛物线于点F,交x轴于点G,设点E的横坐标为m,△ADF的面积为S.求S与m的函数关系式,并求出S的最大值;
(4)若点M为抛物线上异于F的一个动点,在第(3)问△ADF的面积S取最大值的情况下,若S△MAD=3S△ADF,请直接写出M点坐标.

考点:二次函数综合题
专题:压轴题
分析:(1)运用待定系数法即可求出抛物线的解析式.
(2)过点C作直线l的对称点E,过点E作EG⊥AB于G,过点Q作QF∥PE,交EG于点F,连接FB,如图1.易得PC+QB=PE+QB=FQ+QB,根据两点之间线段最短可得:FQ+QB(即PC+QB)最小值为FB,只需在Rt△FGB中运用勾股定理即可解决问题.
(3)运用待定系数法可求出直线AD的解析式,由点E的横坐标为m可用m的代数式表示出点E、F的坐标,从而表示出EF的长,进而表示出△ADF的面积,然后运用配方法就可解决问题.
(4)过点M作MN⊥DH,交直线AD于N,交直线DH于Q,如图3.运用割补法可用MN表示出△ADM的面积,然后根据条件即可得到MN的值.设点M的坐标为(n,-n2-2n+3),则点N的坐标为(n-
,-n2-2n+3),将点N的坐标代入直线AD的解析式,求出n的值,就可得到点M的坐标.
(2)过点C作直线l的对称点E,过点E作EG⊥AB于G,过点Q作QF∥PE,交EG于点F,连接FB,如图1.易得PC+QB=PE+QB=FQ+QB,根据两点之间线段最短可得:FQ+QB(即PC+QB)最小值为FB,只需在Rt△FGB中运用勾股定理即可解决问题.
(3)运用待定系数法可求出直线AD的解析式,由点E的横坐标为m可用m的代数式表示出点E、F的坐标,从而表示出EF的长,进而表示出△ADF的面积,然后运用配方法就可解决问题.
(4)过点M作MN⊥DH,交直线AD于N,交直线DH于Q,如图3.运用割补法可用MN表示出△ADM的面积,然后根据条件即可得到MN的值.设点M的坐标为(n,-n2-2n+3),则点N的坐标为(n-
| 3 |
| 2 |
解答:解:(1)把A(-3,0),B(1,0),C(0,3)代入抛物线y=ax2+bx+c,得:
,
解得:
.
则抛物线的解析式为:y=-x2-2x+3.
(2)过点C作直线l的对称点E,过点E作EG⊥AB于G,过点Q作QF∥PE,交EG于点F,连接FB,如图1.

则有PC=PE,EF∥PQ.
∵EF∥PQ,QF∥PE,
∴四边形EFQP是平行四边形,
∴EF=PQ=1,EP=FQ,
∴PC=FQ,
∴PC+QB=FQ+QB,
根据两点之间线段最短可得:FQ+QB(即PC+QB)最小值为FB.
∵抛物线y=-x2-2x+3的对称轴为x=-1,C(0,3),
∴点E的坐标为(-2,3),
∴点F的坐标为(-2,2).
在Rt△FGB中,
FG=2,GB=1-(-2)=3,
根据勾股定理可得:FB=
=
.
∴PC+QB的最小值为
.
(3)∵抛物线y=-x2-2x+3=-(x+1)2+4,
∴顶点D的坐标为(-1,4) .
.
设直线AD的解析式为y=kx+b,
∵A(-3,0),D(-1,4),
∴
,
解得:
,
∴直线AD的解析式为y=2x+6.
∵点E的横坐标为m,
∴E(m,2m+6),F(m,-m2-2m+3),
∴EF=-m2-2m+3-(2m+6)=-m2-4m-3,
∴S=S△DEF+S△AEF
=
EF•GH+
EF•AG
=
EF•AH
=
(-m2-4m-3)×2
=-m2-4m-3
=-(m+2)2+1,
∴当m=-2时,S最大值为1.
(4)过点M作MN⊥DH,交直线AD于N,交直线DH于Q,如图3.

S△ADM=S△DMN+S△AMN
=
MN•DQ+
MN•QH
=
MN•DH
=2MN.
由题可得:S△ADM=2MN=3,
∴MN=
.
设点M的坐标为(n,-n2-2n+3),
则点N的坐标为(n-
,-n2-2n+3).
∵点N在直线AD上,
∴-n2-2n+3=2(n-
)+6,
整理得:n2+4n=0,
即n(n+4)=0,
解得:n1=0,n2=-4.
∴点M的坐标为(0,3)或(-4,-5).
|
解得:
|
则抛物线的解析式为:y=-x2-2x+3.
(2)过点C作直线l的对称点E,过点E作EG⊥AB于G,过点Q作QF∥PE,交EG于点F,连接FB,如图1.

则有PC=PE,EF∥PQ.
∵EF∥PQ,QF∥PE,
∴四边形EFQP是平行四边形,
∴EF=PQ=1,EP=FQ,
∴PC=FQ,
∴PC+QB=FQ+QB,
根据两点之间线段最短可得:FQ+QB(即PC+QB)最小值为FB.
∵抛物线y=-x2-2x+3的对称轴为x=-1,C(0,3),
∴点E的坐标为(-2,3),
∴点F的坐标为(-2,2).
在Rt△FGB中,
FG=2,GB=1-(-2)=3,
根据勾股定理可得:FB=
| FG2+GB2 |
| 13 |
∴PC+QB的最小值为
| 13 |
(3)∵抛物线y=-x2-2x+3=-(x+1)2+4,
∴顶点D的坐标为(-1,4)
 .
.设直线AD的解析式为y=kx+b,
∵A(-3,0),D(-1,4),
∴
|
解得:
|
∴直线AD的解析式为y=2x+6.
∵点E的横坐标为m,
∴E(m,2m+6),F(m,-m2-2m+3),
∴EF=-m2-2m+3-(2m+6)=-m2-4m-3,
∴S=S△DEF+S△AEF
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
=-m2-4m-3
=-(m+2)2+1,
∴当m=-2时,S最大值为1.
(4)过点M作MN⊥DH,交直线AD于N,交直线DH于Q,如图3.

S△ADM=S△DMN+S△AMN
=
| 1 |
| 2 |
| 1 |
| 2 |
=
| 1 |
| 2 |
=2MN.
由题可得:S△ADM=2MN=3,
∴MN=
| 3 |
| 2 |
设点M的坐标为(n,-n2-2n+3),
则点N的坐标为(n-
| 3 |
| 2 |
∵点N在直线AD上,
∴-n2-2n+3=2(n-
| 3 |
| 2 |
整理得:n2+4n=0,
即n(n+4)=0,
解得:n1=0,n2=-4.
∴点M的坐标为(0,3)或(-4,-5).
点评:本题考查了用待定系数法求二次函数及一次函数的解析式、平行四边形的判定与性质、两点之间线段最短、解一元二次方程、勾股定理等知识,而在解决问题的过程中用到了待定系数法、配方法、割补法、因式分解法等重要的数学方法,是考查学生能力的一道好题.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目
 如图,在△ABC中,AB=AC=3,BC边上有100个不同的点P1,P2…P100,记mi=APi2+BPi•PiC(i=1,2…100),则m1+m2+…+m100的值是( )
如图,在△ABC中,AB=AC=3,BC边上有100个不同的点P1,P2…P100,记mi=APi2+BPi•PiC(i=1,2…100),则m1+m2+…+m100的值是( )| A、300 | B、400 |
| C、800 | D、900 |
下面是同学们所画的数轴,其中正确的是( )
A、 |
B、 |
C、 |
D、 |
 如图,正方形ABCD中,连接BD.点E在边BC上,且CE=2BE.连接AE交BD于F;连接DE,取BD的中点O;取DE的中点G,连接OG.下列结论:
如图,正方形ABCD中,连接BD.点E在边BC上,且CE=2BE.连接AE交BD于F;连接DE,取BD的中点O;取DE的中点G,连接OG.下列结论: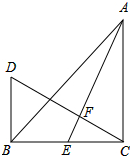 如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D.
如图,在△ABC中,∠ACB=90°,AC=BC,AE是BC的中线,过点C作CF⊥AE于F,过B作BD⊥CB交CF的延长线于点D. 如图,五边形ABCDE中,∠E=∠B=90°,DE+BC=2,DC=AB=AE=2,求这个五边形的面积.
如图,五边形ABCDE中,∠E=∠B=90°,DE+BC=2,DC=AB=AE=2,求这个五边形的面积.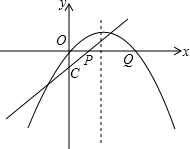 已知直线y=
已知直线y=