��Ŀ����
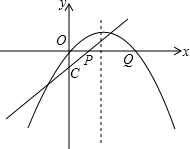
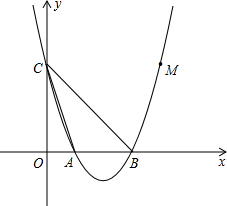 ��ͼ����֪������y=a��x-1����x-3����x��������ҷֱ���A��B���㣬��y�ύ�ڵ�C���������߹���M��4��3��������AC��BC��
��ͼ����֪������y=a��x-1����x-3����x��������ҷֱ���A��B���㣬��y�ύ�ڵ�C���������߹���M��4��3��������AC��BC����1������κ����Ľ���ʽ��
��2����sin��ACB��ֵ��
��3�����߶�BC���Ƿ����һ��Q������Q��QPƽ����y�ύ�������ڵ�P��ʹ�߶�PQȡ�����ֵ��������ڣ������Q�������PQ�����ֵ����������ڣ���˵�����ɣ�
��4������������x���·��IJ�����x�ᷭ�ۣ������ߵ����ಿ�ֱ��ֲ��䣬����M��ֱ��y=kx+b�����ͼ��ֻ���������㣬��bֵ��
���㣺���κ����ۺ���
ר�⣺
��������1���ѵ�M��4��3������������y=a��x-1����x-3�������a=1�����ɵó����κ�������ʽ��
��2�����ö��κ�������ʽΪy=x2-4x+3���ó���A��B�����꣬�ó�AB=2����A��AE��BC��E�����OB=OC���ɵó���OBC=45�㣬���AE��AC�����ɵó�sin��ACB��ֵ��
��3������B��3��0����C��0��3���ó�yBC=-x+3���ٽ�϶��κ�������ʽΪy=x2-4x+3��QPƽ����y�ύ�������ڵ�P�������PQ=-��x-
��2+
�����ɵó���x=
ʱ��PQ�����ֵ��Q�����꣬
��4�������������ֱ��MA���ǹ���M��ֱ����������������ʱ���ֱ����b��ֵ���ɣ�
��2�����ö��κ�������ʽΪy=x2-4x+3���ó���A��B�����꣬�ó�AB=2����A��AE��BC��E�����OB=OC���ɵó���OBC=45�㣬���AE��AC�����ɵó�sin��ACB��ֵ��
��3������B��3��0����C��0��3���ó�yBC=-x+3���ٽ�϶��κ�������ʽΪy=x2-4x+3��QPƽ����y�ύ�������ڵ�P�������PQ=-��x-
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
��4�������������ֱ��MA���ǹ���M��ֱ����������������ʱ���ֱ����b��ֵ���ɣ�
����⣺��1���ѵ�M��4��3������������y=a��x-1����x-3������3=a��4-1����4-3�������a=1��
���Զ��κ�������ʽΪy=��x-1����x-3��=x2-4x+3��
��2����ͼ1��
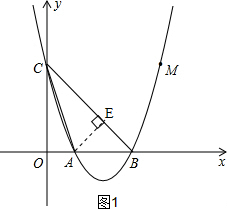
�߶��κ�������ʽΪy=x2-4x+3��
��x2-4x+3=0�����x1=1��x2=3��
���A��1��0����B��3��0����AB=2��
��A��AE��BC��E��
�߶��κ�������ʽΪy=x2-4x+3��
��x=0ʱ��y=3��
��OB=OC=3��
���OBC=45�㣬
��AE=
��
��AC=
=
��
��sin��ACB=
=
=
��
��3����B��3��0����C��0��3����BC���ڵ�ֱ��Ϊy=kx+b�������yBC=-x+3��
�߶��κ�������ʽΪy=x2-4x+3��QPƽ����y�ύ�������ڵ�P��
��PQ=��-x+3��-��x2-4x+3��=-x2+3x=-��x-
��2+
�൱x=
ʱ��PQ�����ֵΪ
����ʱQ��
��
����
��4����ͼ2��
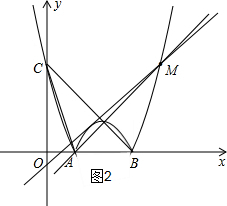
��ֱ��MA�����������������㣬��ֱ��MA�Ľ���ʽΪy=kx+b����A��1��0����M��4��3�����ɵ�
y=x-1������b=-1��
���������߶���Ϊ��2��1��������ʽΪy=-��x-2��2+1=-x2+4x-3����M��4��3������ֱ��y=kx+b����b=3-4k��
����
����x2+��k-4��x+6-4k=0���ɡ�=0��k2+8k-8=0����õ�k=-4��2
���Ḻ����b=3-4k=19-8
��
����������b=-1��b=19-8
��
���Զ��κ�������ʽΪy=��x-1����x-3��=x2-4x+3��
��2����ͼ1��

�߶��κ�������ʽΪy=x2-4x+3��
��x2-4x+3=0�����x1=1��x2=3��
���A��1��0����B��3��0����AB=2��
��A��AE��BC��E��
�߶��κ�������ʽΪy=x2-4x+3��
��x=0ʱ��y=3��
��OB=OC=3��
���OBC=45�㣬
��AE=
| 2 |
��AC=
| OA2+OC2 |
| 10 |
��sin��ACB=
| AE |
| AC |
| ||
|
| ||
| 5 |
��3����B��3��0����C��0��3����BC���ڵ�ֱ��Ϊy=kx+b�������yBC=-x+3��
�߶��κ�������ʽΪy=x2-4x+3��QPƽ����y�ύ�������ڵ�P��
��PQ=��-x+3��-��x2-4x+3��=-x2+3x=-��x-
| 3 |
| 2 |
| 9 |
| 4 |
�൱x=
| 3 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
��4����ͼ2��

��ֱ��MA�����������������㣬��ֱ��MA�Ľ���ʽΪy=kx+b����A��1��0����M��4��3�����ɵ�
y=x-1������b=-1��
���������߶���Ϊ��2��1��������ʽΪy=-��x-2��2+1=-x2+4x-3����M��4��3������ֱ��y=kx+b����b=3-4k��
����
|
| 6 |
| 6 |
����������b=-1��b=19-8
| 6 |
������������Ҫ�����˶��κ���ͼ������������ͼ���������⣬�ѵ��ǵڣ�4�������⣬Ҫ�������������Ĺؼ��ǽ��ͼ���ҳ�ֱ�ߵ�λ�ã�

��ϰ��ϵ�д�
 ֥�鿪���γ�������ϵ�д�
֥�鿪���γ�������ϵ�д� ����ѧ��ţ��Ӣ��ϵ�д�
����ѧ��ţ��Ӣ��ϵ�д�
�����Ŀ
 ��ͼ��������ABCD�У�����BD����E�ڱ�BC�ϣ���CE=2BE������AE��BD��F������DE��ȡBD���е�O��ȡDE���е�G������OG�����н��ۣ�
��ͼ��������ABCD�У�����BD����E�ڱ�BC�ϣ���CE=2BE������AE��BD��F������DE��ȡBD���е�O��ȡDE���е�G������OG�����н��ۣ� ��ͼ�������ABCDE�У���E=��B=90�㣬DE+BC=2��DC=AB=AE=2�����������ε������
��ͼ�������ABCDE�У���E=��B=90�㣬DE+BC=2��DC=AB=AE=2�����������ε������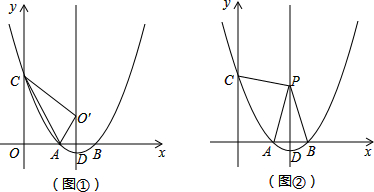
 ��ֱ֪��y=
��ֱ֪��y=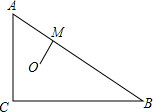 ��ͼ����ABC�У���C=90�㣬AC=6��BC=8��OΪ��ABC�����ģ�OM��AB��M����OM�ij���
��ͼ����ABC�У���C=90�㣬AC=6��BC=8��OΪ��ABC�����ģ�OM��AB��M����OM�ij���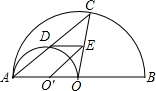 ��ͼ��AB�ǰ�ԲO��ֱ������OAΪֱ���İ�ԲO������AC���ڵ�D��O��E��AC������OC�ڵ�E���������ĸ����ۣ��ٵ�DΪAC���е㣻��S��O��OE=
��ͼ��AB�ǰ�ԲO��ֱ������OAΪֱ���İ�ԲO������AC���ڵ�D��O��E��AC������OC�ڵ�E���������ĸ����ۣ��ٵ�DΪAC���е㣻��S��O��OE=