题目内容
17. 如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是CD的中点,AC与BE交于点F,那么△ABF和△CEF的面积比是6:1.
如图,在梯形ABCD中,AD∥BC,BC=2AD,点E是CD的中点,AC与BE交于点F,那么△ABF和△CEF的面积比是6:1.
分析 延长BE,AD交于G,根据平行线的性质得到∠G=∠EBC,根据全等三角形的性质得到DG=BC=2AD,GE=BE,于是得到AG=3AD,通过△AGF∽△BCF,得到$\frac{AF}{CF}=\frac{GF}{BF}=\frac{AG}{BC}$=$\frac{3}{2}$,设GF=3x,BF=2x,求得$\frac{BF}{EF}=\frac{4}{1}$,由$\frac{{S}_{△ABF}}{{S}_{△BCF}}$=$\frac{AF}{CF}$=$\frac{3}{2}$,得到S△ABF=$\frac{3}{2}$S△BCF,由$\frac{{S}_{△BCF}}{{S}_{△CEF}}$=$\frac{BF}{EF}$=4,得到S△CEF=$\frac{1}{4}$S△BCF,即可得到结论.
解答  解:延长BE,AD交于G,
解:延长BE,AD交于G,
∵AD∥BC,
∴∠G=∠EBC,
在△DGE与△BCE中,
$\left\{\begin{array}{l}{∠G=∠EBC}\\{∠DEG=∠BEC}\\{DE=CE}\end{array}\right.$,
∴DG=BC=2AD,GE=BE,
∴AG=3AD,
∵AD∥BC,
∴△AGF∽△BCF,
∴$\frac{AF}{CF}=\frac{GF}{BF}=\frac{AG}{BC}$=$\frac{3}{2}$,
∴设GF=3x,BF=2x,
∴BG=5x,
∴BE=GE=2.5x,
∴EF=$\frac{1}{2}$x,
∴$\frac{BF}{EF}=\frac{4}{1}$,
∴$\frac{{S}_{△ABF}}{{S}_{△BCF}}$=$\frac{AF}{CF}$=$\frac{3}{2}$,
∴S△ABF=$\frac{3}{2}$S△BCF,
∵$\frac{{S}_{△BCF}}{{S}_{△CEF}}$=$\frac{BF}{EF}$=4,
∴S△CEF=$\frac{1}{4}$S△BCF,
∴△ABF和△CEF的面积比=$\frac{\frac{3}{2}{S}_{△BCF}}{\frac{1}{4}{S}_{△BCF}}$=6:1.
故答案为:6:1.
点评 本题考查了相似三角形的判定和性质,全等三角形的判定和性质,平行线的性质,正确的作出辅助线是解题的关键.

 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案 如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是B;当字母C第201次出现时,恰好数到的数是603.
如图为手的示意图,在各个手指间标记字母A、B、C、D.请你按图中箭头所指方向(即A→B→C→D→C→B→A→B→C→…的方式)从A开始 数连续的正整数1,2,3,4…,当数到12时,对应的字母是B;当字母C第201次出现时,恰好数到的数是603. 如图,在△ABC中,AB=AC,BC=6,点E,F是中线AD上两点,AD=4,则图中阴影面积是6.
如图,在△ABC中,AB=AC,BC=6,点E,F是中线AD上两点,AD=4,则图中阴影面积是6. 如图,有一条两岸平行的河流,一数学实践活动小组在无法涉水过河情况下,成功测得河的宽度,他们的做法如下:
如图,有一条两岸平行的河流,一数学实践活动小组在无法涉水过河情况下,成功测得河的宽度,他们的做法如下: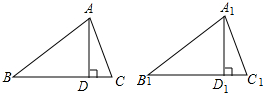 如图所示,AD、A1D1分别是锐角△ABC和△A1B1C1中边BC、B1C1的高,且AB=A1B1,AD=A1D1,若要使△ABC≌△A1B1C1,可补充的条件是∠C=∠C1(只需要填写一个你认为适当的条件即可)
如图所示,AD、A1D1分别是锐角△ABC和△A1B1C1中边BC、B1C1的高,且AB=A1B1,AD=A1D1,若要使△ABC≌△A1B1C1,可补充的条件是∠C=∠C1(只需要填写一个你认为适当的条件即可) 如图,直线l1、l2相交于点A(2,3),l1与x轴的交点B坐标为(-1,0),l2与y轴的交点坐标为(0,-2),结合图象解答下列问题:
如图,直线l1、l2相交于点A(2,3),l1与x轴的交点B坐标为(-1,0),l2与y轴的交点坐标为(0,-2),结合图象解答下列问题: