Question

12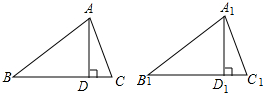．如图所示，AD、A₁D₁分别是锐角△ABC和△A₁B₁C₁中边BC、B₁C₁的高，且AB=A₁B₁，AD=A₁D₁，若要使△ABC≌△A₁B₁C₁，可补充的条件是∠C=∠C₁（只需要填写一个你认为适当的条件即可）

Answer 1

分析 根据HL推出Rt△ADB≌Rt△A₁D₁B₁，根据全等三角形的性质得出∠B=∠B₁，根据AAS推出全等即可．

解答 解：∠C=∠C₁，
理由是：∵AD、A₁D₁分别是锐角△ABC和△A₁B₁C₁中边BC、B₁C₁的高，
∴∠ADB=∠A₁D₁B₁=90°，
在Rt△ADB和Rt△A₁D₁B₁中
$\left\{\begin{array}{l}{AB={A}_{1}{B}_{1}}\\{AD=A{{\;}_{1}D}_{1}}\end{array}\right.$
∴Rt△ADB≌Rt△A₁D₁B₁（HL），
∴∠B=∠B₁，
在△ABC和△A₁B₁C₁中
$\left\{\begin{array}{l}{∠C=∠{C}_{1}}\\{∠B=∠{B}_{1}}\\{AB={A}_{1}{B}_{1}}\end{array}\right.$
∴△ABC≌△A₁B₁C₁（AAS），
故答案为：∠C=∠C₁．

点评 本题考查了全等三角形的判定定理的应用，能熟练地掌握全等三角形的判定定理和性质定理是解此题的关键，注意：全等三角形的判定定理有：SAS，ASA，AAS，SSS，此题是一道开放型的题目，答案不唯一．