Question

20．已知：在直角三角形ABC中，MN为斜边AB的中垂线，M为垂足，MN与Rt∠ACB的平分线交于点N．求证：∠MCN=∠MNC．

Answer 1

分析 根据直角三角形斜边上的中线等于斜边的一半可得AM=CM，再根据角平分线的性质及三角形的外角性质可得∠CMB=2∠ACM，最后根据三角形内角和定理可得到∠MCN=∠MNC．

解答 证明：如图，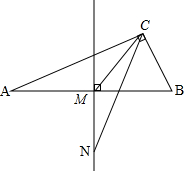

∵MN是AB的中垂线，
∴CM是斜边AB上的中线，
∴AM=CM，
∴∠A=∠ACM，
∵CN是Rt∠ACB的角平分线，
∴∠ACN=45°，
∴∠MCN=45°-∠ACM，
∵∠CMB是△AMC的外角，
∴∠CMB=2∠ACM，
∵MN⊥AB，
∴∠CMN=90°+2∠ACM，
∵∠CMN+∠MNC+∠MCN=180°，
∴∠MNC=45°-∠ACM，
∴∠MCN=∠MNC．

点评 此题主要考查直角三角形性质、三角形内角和定理、三角形的外角性质，掌握这些基本性质和定理是解题的关键．