题目内容
10.(1)计算:|$\sqrt{3}$-2|+20090-(-$\frac{1}{3}$)-1+3tan30°;(2)解方程:$\frac{2x}{2x-1}$+$\frac{5}{1-2x}$=3.
分析 (1)原式利用绝对值的代数意义,零指数幂、负整数指数幂法则,以及特殊角的三角函数值计算即可得到结果;
(2)分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:(1)原式=2-$\sqrt{3}$+1-(-3)+3×$\frac{\sqrt{3}}{3}$=2-$\sqrt{3}$+1+3+$\sqrt{3}$=6;
(2)去分母得:2x-5=6x-3,
解得:x=-$\frac{1}{2}$,
经检验x=-$\frac{1}{2}$是分式方程的解.
点评 此题考查了解分式方程,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
20.三个有理数相乘积为负数,则其中负因数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 1个或3个 |
18.当a>0时,下列关于幂的运算正确的是( )
| A. | a0=1 | B. | a-1=-a | C. | (-a)2=-a2 | D. | (ab)2=ab2 |
19.在△ABC中,∠C=90°,tanA=$\frac{3}{4}$,则sinB,cosB,tanB中最小的是( )
| A. | tanB | B. | sinB | C. | cosB | D. | sinB或cosB |
 如图所示,作字母H关于坐标原点的中心对称图形,并写出所得图形相应各点的坐标.
如图所示,作字母H关于坐标原点的中心对称图形,并写出所得图形相应各点的坐标.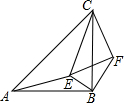 如图,点E在△ABC内,△EFC∽△ABC,∠ABC=∠EFC=90°,∠CAE+∠CBE=90°,连接BF,求证:∠EBF=90°.
如图,点E在△ABC内,△EFC∽△ABC,∠ABC=∠EFC=90°,∠CAE+∠CBE=90°,连接BF,求证:∠EBF=90°.