题目内容
2.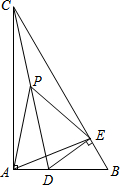 如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.
如图,Rt△ABC中,∠CAB=90°,∠ACB=30°,D是AB上一点(不与A、B重合),DE⊥BC于E,若P是CD的中点,请判断△PAE的形状,并说明理由.
分析 由直角三角斜边上的中线性质得出PA=PC=$\frac{1}{2}$CD,由等腰三角形的性质和三角形的外角性质得出∠APD=2∠ACD,同理得出∠DPE=2∠DCB,PA=PE,再证出∠APE=2∠ACB=60°,即可得出结论.
解答 解:△PAE的形状为等边三角形;理由如下:
∵在Rt△CAD中,∠CAD=90°,P是斜边CD的中点,
∴PA=PC=$\frac{1}{2}$CD,
∴∠ACD=∠PAC,
∴∠APD=∠ACD+∠PAC=2∠ACD,
同理:在Rt△CED中,PE=PC=$\frac{1}{2}$CD,∠DPE=2∠DCB,
∴PA=PE,即△PAE是等腰三角形,
∴∠APE=2∠ACB=2×30°=60°,
∴△PAE是等边三角形.
点评 本题考查了等边三角形的判定、直角三角斜边上的中线性质、等腰三角形的判定;熟练掌握等边三角形的判定方法,由直角三角斜边上的中线性质得出PA=PC,PE=PC是解决问题的关键.

练习册系列答案
 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案
相关题目
12.下列等式正确的是( )
| A. | (-1)0=-1 | B. | (-1)-1=1 | C. | 2x-2=$\frac{1}{{2{x^2}}}$ | D. | x-2y2=$\frac{y^2}{x^2}$ |
17. 如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
 如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )
如图,点E、F在AC上,AD=BC,DF=BE,要使△ADF≌△CBE,还需要添加一个条件是( )| A. | AD∥BC | B. | DF∥BE | C. | ∠D=∠B | D. | ∠A=∠C |
7.将二次函数y=x2-6x+5用配方法化成y=(x-h)2+k的形式,下列结果中正确的是( )
| A. | y=(x-6)2+5 | B. | y=(x-3)2+5 | C. | y=(x-3)2-4 | D. | y=(x+3)2-9 |
12.设2+$\sqrt{3}$的整数部分用a表示,小数部分用b表示,4-$\sqrt{3}$的整数部分用c表示,小数部分用d表示,则$\frac{b+d}{ac}$的值为( )
| A. | $\frac{1}{8}$ | B. | $\frac{1}{6}$ | C. | $\frac{5}{6}$ | D. | $\frac{1}{3}$($\sqrt{3}$-1) |