题目内容
8.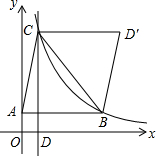 如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.
如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.
分析 设AB交CD于H.首先证明B、C关于直线y=x对称,设C(a,b),则B(b,a),想办法列出方程求出k即可.
解答 解:设AB交CD于H.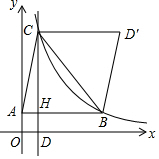
由题意AB=CD′=CD,
∴B、C两点关于直线y=x对称,设C(a,b),则B(b,a),
∵S△ABC=$\frac{3k}{2}$,
∴$\frac{1}{2}$•b•(b-a)=$\frac{3k}{2}$,∵ab=k,
∴b=2$\sqrt{k}$,a=$\frac{1}{2}$$\sqrt{k}$,
∴CH=BH=$\frac{3}{2}$$\sqrt{k}$,
∵BC=$\frac{3k}{4}$,
∴BC=$\sqrt{2}$BH,
∴$\frac{3}{4}$k=$\sqrt{2}$•$\frac{3}{2}$$\sqrt{k}$,
解得k=8.
故答案为8.
点评 本题考查反比例函数图象上点的特征、k的几何意义、平行四边形的性质等知识,解题的关键是学会利用参数,构建方程解决问题,属于中考填空题中的压轴题.

练习册系列答案
相关题目
16.如图,在平面直角坐标系中,已知点A(-3,0),B(0,4),AB=5,对△AOB连续旋转变换,依次得到△1,△2,△3,△4…,则△2017的直角顶点的坐标为( )


| A. | (4032,0) | B. | (4036,0) | C. | (8064,0) | D. | (8068,0) |
17.已知函数y=(m+1)x+m的函数值y随自变量x的增大而减小,那么m的取值范围是( )
| A. | m>-1 | B. | m<-1 | C. | m<1 | D. | m<0 |
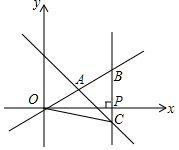 在平面直角坐标系xOy中,一次函数y=-x+7的图象交y轴于点D,且它与正比例函数y=$\frac{3}{4}$x的图象交于点A.
在平面直角坐标系xOy中,一次函数y=-x+7的图象交y轴于点D,且它与正比例函数y=$\frac{3}{4}$x的图象交于点A.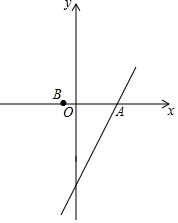 已知抛物线y1=a(x-x1)(x-x2)(a≠0,x1≠x2)与x轴分别交于A(x1,0)、
已知抛物线y1=a(x-x1)(x-x2)(a≠0,x1≠x2)与x轴分别交于A(x1,0)、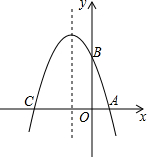 如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4.
如图,在平面直角坐标系中,抛物线y=ax2+bx+3与x轴交于A、C两点,与y轴交于点B,且OA=1,OC=4. (1)已知二次函数y1=-(x+1)2+4的图象如图所示,请在同一坐标系中画出二次函数y1=-(x-2)2+1的图象.
(1)已知二次函数y1=-(x+1)2+4的图象如图所示,请在同一坐标系中画出二次函数y1=-(x-2)2+1的图象.