题目内容
20. (1)已知二次函数y1=-(x+1)2+4的图象如图所示,请在同一坐标系中画出二次函数y1=-(x-2)2+1的图象.
(1)已知二次函数y1=-(x+1)2+4的图象如图所示,请在同一坐标系中画出二次函数y1=-(x-2)2+1的图象.(2)平行于x轴的直线y=k在抛物线y2=-(x-2)2+1上截得线段AB=4,求抛物线y2=-(x-2)2+1的顶点到线段AB的距离.
(3)当-1<x<2时,利用函数图象比较y1与y2的大小.
分析 (1)根据图象平移的规律,可得答案;
(2)解方程组得到A(2+$\sqrt{1-k}$,k),B(2-$\sqrt{1-k}$,k),求得k=-3,于是得到结论;
(3)根据图象即可得到结论.
解答 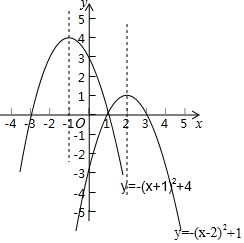 解 (1)如图所示,
解 (1)如图所示,
(2)解$\left\{\begin{array}{l}{y=k}\\{y=-(x-2)^{2}+1}\end{array}\right.$得,$\left\{\begin{array}{l}{x=2+\sqrt{1-k}}\\{y=k}\end{array}\right.$或$\left\{\begin{array}{l}{x=2-\sqrt{1-k}}\\{y=k}\end{array}\right.$,
∴A(2+$\sqrt{1-k}$,k),B(2-$\sqrt{1-k}$,k),
∵AB=4,
∴2$\sqrt{1-k}$=4,
∴k=-3,
∵抛物线y2=-(x-2)2+1的顶点坐标为(2,1),
∴抛物线y2=-(x-2)2+1的顶点到线段AB的距离=4;
(3)当-1<x<1时,y1>y2.当x=1时,y1=y2.当1<x<2时,y1<y2.
点评 题考查了二次函数图象,利用图象平移的规律:左加右减,上加下减.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.下列运算正确的是( )
| A. | (ab)2=ab2 | B. | 3a+2a2=5a2 | C. | (2x2)3=6x6 | D. | a2•a=a3 |
11. 如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )
如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )
 如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )
如图,一个粒子在第一象限内及x、y轴上运动,在第一分钟内它从原点O运动到(1,0),而后它接着按图所示在与x轴、y轴平行的方向上来回运动,且每分钟移动1个长度单位,那么2017分钟后这个粒子所处的位置是( )| A. | (7,45) | B. | (8,44) | C. | (44,7) | D. | (45,8) |
15.在反比例函数y=$\frac{m-1}{x}$的图象的每个分支上,y都随x的增大而减少,则实数m的取值范围是( )
| A. | m>1 | B. | m>0 | C. | m<1 | D. | m<0 |
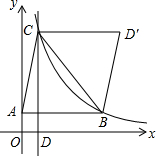 如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8.
如图,在△ABC中,B、C两点恰好在反比例函数y=$\frac{k}{x}$(k>0)第一象限的图象上,且BC=$\frac{3k}{4}$,S△ABC=$\frac{3k}{2}$,AB∥x轴,CD⊥x轴交x轴于点D,作D关于直线BC的对称点D′.若四边形ABD′C为平行四边形,则k为8. “六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.
“六一”儿童节期间,甲、乙两家网店以同样价格销售相同的儿童用品,他们的优惠方案分别为:甲店,一次性购物超过100元后的价格部分打七折;乙店,一次性购物超过500元后的价格部分打五折.设商品原价为x元,购物应付金额为y元.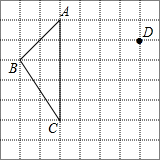 如图,在方格纸中,已知格点△ABC及其外一点D,平移△ABC,使点A移动到点D.完成下列作图:
如图,在方格纸中,已知格点△ABC及其外一点D,平移△ABC,使点A移动到点D.完成下列作图: 已知:如图,把△A′B′C′向下平移3个单位长度,再向左平移2个单位长度,得到△ABC.
已知:如图,把△A′B′C′向下平移3个单位长度,再向左平移2个单位长度,得到△ABC.