题目内容
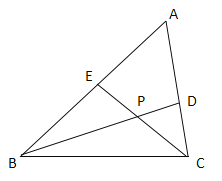
【题目】如图,在![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 和
和![]() 的平分线,
的平分线,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() 于
于![]() ,交
,交![]() 于
于![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,结论①
,结论①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )
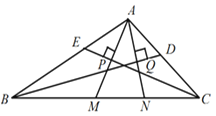
A.4个B.3个C.2个D.1个
【答案】B
【解析】
①根据三角形的内角和定理判定∠CAM=∠CMA,由等腰三角形的判定和三线合一的性质可得结论正确;
②根据BN=AB=6,CM=AC=5,及线段的和与差可得BC的长;
③根据三角形的内角和定理及角的和与差可得结论;
④要想得到AM=AN,必有∠AMN=∠ANM,而AB≠AC,可知∠ABC≠∠ACB,从而得AM≠AN.
解:①∵CE平分∠ACE,
∴∠ACP=∠MCP,
∵AM⊥CE,
∴∠APC=∠MPC=90°,
∴∠CAM=∠CMA,
∴AC=CM,
∴AP=PM,
①正确;
②同理得:BN=AB=6,
∵CM=AC=5,
∴BC=BN+CM-MN=6+5-2=9,
②正确;
③∵∠BAC=∠MAC+∠BAN-∠MAN=110°,
由①知:∠CMA=∠CAM,∠BNA=∠BAN,
△AMN中,∠CMA+∠BNA=180°-∠MAN=∠BAN+∠MAC,
∴180°-∠MAN-∠MAN=110°,
∴∠MAN=35°,
③正确;
④当∠AMN=∠ANM时,AM=AN,
∵AB=6≠AC=5
∴∠ABC≠∠ACB,
∴∠AMN≠∠ANM,则AM与AN不相等,
④不正确;
所以本题不正确的有④,
故选:B.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目