Question

【题目】如图，在等腰直角三角形中，，，.将等腰直角形沿高剪开后，拼成图2所示的正方形.

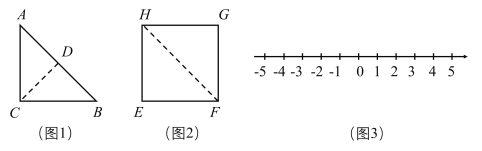
(1)如图1，等腰直角三角形的面积是______________.

(2)如图2，求正方形的边长是多少？

(3)把正方形放到数轴上(如图3)，使得边落到数轴上，其中一个端点所对应的数为-1，直接写出另一个端点所对应的数.

Answer 1

【答案】（1）8；（2）（3）-1+或-1-

【解析】

（1）根据面积公式进行计算；

（2）根据所拼图形，可知正方形的边长为△ABC的高，从而计算可得；

（3）根据（2）中所求边长，当点E在-1，和点F在-1处分别得出另一个点对应的数.

解：（1）==8；

（2）由题意可知，拼成正方形EFGH后，

△ABC的高CD变成了正方形的边长，

∵CD===，

∴正方形EFGH的边长为；

（3）当点E在-1处时，

F所对应的数为：-1+，

当点F在-1处时，

F所对应的数为：-1-，

∴另一个端点所对应的的数为-1+或-1-.