Question

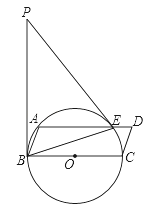
【题目】如图1，将等腰△ABC沿对称轴折叠后，得到△ADC（△ADB），若，则称等腰△ABC为“长月三角形”ABC.

（1）结合题目情境，请你判断“长月三角形”一定会是______三角形.

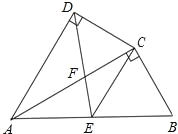
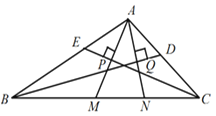
（2）如图2，C为线段AB上一点，分别以AC和BC为边作“长月三角形”ACD和“长月三角形”BCE，连接AE、BD交于点O，AE与CD交于点P，CE与BD交于点M.

①求证：；

②求的度数.

Answer 1

【答案】（1）等边；（2）①见解析；②120°

【解析】

（1）利用等腰三角形性质以及含30°的直角三角形进行判断即可.

（2）①利用（1）中结论，易证，即可解答；

②利用全等三角形对应角相等的性质，即可解答.

（1）等边；

证明：∵将等腰△ABC沿对称轴折叠

∴AD⊥CD ∴△ADC为直角三角形

∵

∴∠A=30°，∠C=60°

∴等腰△ABC为等边三角形.

∴“长月三角形”一定会是等边三角形.

（2）①由（1）可知，△ACD和△BCE是等边三角形

∴AC=CD，CE=CB，∠ACD=∠BCE=60°

∴∠ACD+∠DCE=∠BCE+∠DCE 即∠ACE=∠BCD

在和中，

∴

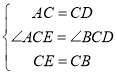
∴AE=BD

②∵

∴∠CAE=∠CDB

∵∠DCA=∠CDB+∠DBC=60°

∴∠DOA=∠CAE+∠DBC=60°

∵∠DOA+∠AOB=180°

∴∠AOB=120°