题目内容
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() 轴,且经过(0,0),(
轴,且经过(0,0),(![]() )两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
)两点,点P在抛物线上运动,以P为圆心的⊙P经过定点A(0,2),
(1)求![]() 的值;
的值;
(2)求证:点P在运动过程中,⊙P始终与![]() 轴相交;
轴相交;
(3)设⊙P与![]() 轴相交于M
轴相交于M![]() ,N
,N ![]() (
(![]() <
<![]() )两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
)两点,当△AMN为等腰三角形时,求圆心P的纵坐标.
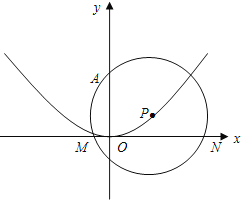
【答案】(1)a=![]() ,b=c=0;(2)证明见解析;(3)P的纵坐标为0或4+2
,b=c=0;(2)证明见解析;(3)P的纵坐标为0或4+2![]() 或4﹣2
或4﹣2![]() .
.
【解析】试题分析:(1)根据题意得出二次函数一般形式进而将已知点代入求出a,b,c的值即可;
(2)设P(x,y),表示出⊙P的半径r,进而与![]() x2比较得出答案即可;
x2比较得出答案即可;
(3)分别表示出AM,AN的长,进而分别利用当AM=AN时,当AM=MN时,当AN=MN时,求出a的值,进而得出圆心P的纵坐标即可.
试题解析:(1)∵抛物线y=ax2+bx+c(a,b,c是常数,a≠0)的对称轴为y轴,且经过(0,0)和(![]() ,
, ![]() )两点,
)两点,
∴抛物线的一般式为:y=ax2,
∴![]() =a(
=a(![]() )2,
)2,
解得:a=±![]() ,
,
∵图象开口向上,∴a=![]() ,
,
∴抛物线解析式为:y=![]() x2,
x2,
故a=![]() ,b=c=0;
,b=c=0;
(2)设P(x,y),⊙P的半径r=![]() ,
,
又∵y=![]() x2,则r=
x2,则r=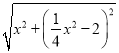 ,
,
化简得:r=![]() >
>![]() x2,
x2,
∴点P在运动过程中,⊙P始终与x轴相交;
(3)设P(a, ![]() a2),∵PA=
a2),∵PA=![]() ,
,
作PH⊥MN于H,则PM=PN=![]() ,
,
又∵PH=![]() a2,
a2,
则MH=NH=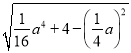 =2,
=2,
故MN=4,
∴M(a﹣2,0),N(a+2,0),
又∵A(0,2),∴AM=![]() ,AN=
,AN=![]() ,
,
当AM=AN时, ![]() =
=![]() ,
,
解得:a=0,
当AM=MN时, ![]() =4,
=4,
解得:a=2±2![]() (负数舍去),则
(负数舍去),则![]() a2=4+2
a2=4+2![]() ;
;
当AN=MN时, ![]() =4,
=4,
解得:a=﹣2±2![]() (负数舍去),则
(负数舍去),则![]() a2=4﹣2
a2=4﹣2![]() ;
;
综上所述,P的纵坐标为0或4+2![]() 或4﹣2
或4﹣2![]() .
.


练习册系列答案
相关题目