Question

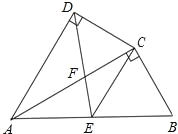
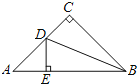
【题目】如图，为等边三角形，为上的一个动点，为延长线上一点，且．

（1）当是的中点时，求证：．

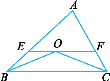
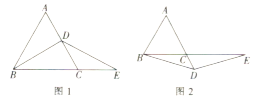
（2）如图1，若点在边上，猜想线段与之间的关系，并说明理由．

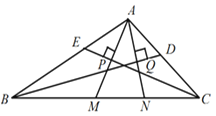
（3）如图2，若点在的延长线上，（1）中的结论是否仍然成立，请说明理由．

Answer 1

【答案】（1）证明见解析；（2），理由见解析；（3）成立，理由见解析．

【解析】

（1）根据等边三角形的性质可得，，然后根据等边对等角可得，从而求出，然后利用等角对等边即可证出，从而证出结论；

（2）过点作，交于点，根据等边三角形的判定也是等边三角形，然后利用AAS即可证出，根据全等三角形的性质可得，从而证出结论；

（3）过点作，交的延长线于点,根据等边三角形的判定也是等边三角形，然后利用AAS即可证出，根据全等三角形的性质可得，从而证出结论；

（1）证明：∵为等边三角形，是的中点，

∴，．

∵，

∴．

∵，

∴，

∴，

∴．

（2）．

理由：如图，过点作，交于点．

∵是等边三角形，

∴也是等边三角形，

∴，．

∵，

∴．

∵，

∴，

∴．

又∵，，

∴．

在和中，

∴，

∴，

∴．

（3）如图，过点作，交的延长线于点．

∵是等边三角形，

∴也是等边三角形，

∴，．

∵，

∴．

∵，

∴，

∴，

在和中，

∴，

∴，

∴．