题目内容
如图,在⊙O上位于直径AB的异侧有定点C和动点P,点P在半圆弧AB上运动(不与A、B两点重合),过点C作CD⊥PB,垂足为D点.
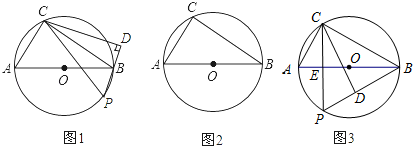
(1)如图1,求证:△PCD∽△ABC;
(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;
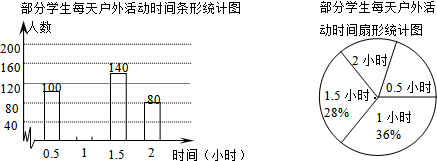
(3)如图3,若AC=
AB,当点P运动到CP⊥AB时,求∠BCD的度数.

(1)如图1,求证:△PCD∽△ABC;
(2)当点P运动到什么位置时,△PCD≌△ABC?请在图2中画出△PCD并说明理由;
(3)如图3,若AC=
| 1 |
| 2 |
考点:相似三角形的判定与性质,全等三角形的判定与性质,圆周角定理
专题:
分析:(1)由AB是⊙O的直径,根据直径对的圆周角是直角,即可得∠ACB=90°,又由PD⊥CD,可得∠D=∠ACB,又由在同圆或等圆中,同弧或等弧所对的圆周角相等,即可得∠A=∠P,根据有两角对应相等的三角形相似,即可判定:△PCD∽△ABC;
(2)由△PCD∽△ABC,可知当PC=AB时,△PCD≌△ABC,利用相似比等于1的相似三角形全等即可求得;
(3)由∠ACB=90°,AC=
AB,可求得∠ABC的度数,然后利用相似,即可得∠PCD的度数,又由垂径定理,求得弧AC=弧AP,然后利用圆周角定理求得∠ACP的度数,继而求得答案.
(2)由△PCD∽△ABC,可知当PC=AB时,△PCD≌△ABC,利用相似比等于1的相似三角形全等即可求得;
(3)由∠ACB=90°,AC=
| 1 |
| 2 |
解答:(1)证明:∵AB是⊙O的直径
∴∠ACB=90°
∵PD⊥CD
∴∠D=90°
∴∠D=∠ACB
∵∠A与∠P是弧BC所对的圆周角
∴∠A=∠P
∴△PCD∽△ABC
(2)解:当PC是⊙O的直径时,△PCD≌△ABC.理由如下:
∵AB、PC是⊙O的半径
∴AB=PC
∴△PCD≌△ABC(AAS)
画图如下:
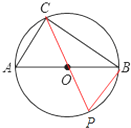
(3)解:∵∠ACB=90°,AC=
AB
∴∠ABC=30°,
∵△PCD∽△ABC,
∴∠PCD=∠ABC=30°,
∵CP⊥AB,AB是⊙O的直径,
∴弧AC=弧AP
∴∠ACP=∠ABC=30°,
∴∠BCD=∠ACB-∠ACP-∠PCD=90°-30°-30°=30°.
∴∠ACB=90°
∵PD⊥CD
∴∠D=90°
∴∠D=∠ACB
∵∠A与∠P是弧BC所对的圆周角
∴∠A=∠P
∴△PCD∽△ABC
(2)解:当PC是⊙O的直径时,△PCD≌△ABC.理由如下:
∵AB、PC是⊙O的半径
∴AB=PC
∴△PCD≌△ABC(AAS)
画图如下:

(3)解:∵∠ACB=90°,AC=
| 1 |
| 2 |
∴∠ABC=30°,
∵△PCD∽△ABC,
∴∠PCD=∠ABC=30°,
∵CP⊥AB,AB是⊙O的直径,
∴弧AC=弧AP
∴∠ACP=∠ABC=30°,
∴∠BCD=∠ACB-∠ACP-∠PCD=90°-30°-30°=30°.
点评:本题考查了圆周角定理、垂径定理、相似三角形的判定与性质、全等三角形的判定与性质以及直角三角形的性质等知识.此题综合性较强,难度适中,注意数形结合思想的应用.

练习册系列答案
相关题目
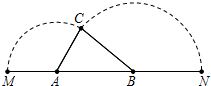 如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x.
如图,已知A、B是线段MN上的两点,MN=4,MA=1,MB>1.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设AB=x. 如图,∠1=
如图,∠1=