题目内容
在平面直角坐标系xOy中,直线l与直线y=-2x关于y轴对称,直线l与反比例函数y=
的图象的一个交点为A(2,m).
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
| k |
| x |
(1)试确定反比例函数的表达式;
(2)若过点A的直线与x轴交于点B,且∠ABO=45°,直接写出点B的坐标.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)求出直线l的解析式,求出A的坐标,把A的坐标代入求出即可;
(2)根据等腰三角形性质得出AM=BM=4,即可得出答案.
(2)根据等腰三角形性质得出AM=BM=4,即可得出答案.
解答:解:(1)由题意,直线l与直线y=-2x关于y轴对称,
∴直线l的解析式为y=2x,
∵点A(2,m)在直线l上,
∴m=2×2=4.
∴点A的坐标为(2,4),
又∵点A(2,4)在反比例函数y=
的图象上,
∴4=
,
∴k=8.
∴反比例函数的解析式为y=
;
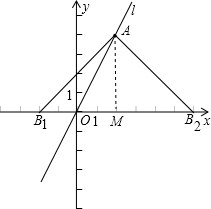
(2)过A作AM⊥x轴于M,
∵A(2,4),
∴AM=4,OM=2,∠AMB=90°,
∴∠ABO=∠BAM=45°,
∴MB2=MB1=AM=4,
∴B2的坐标是(6,0),B1的坐标是(-2,0),
即B的坐标是(6,0)或(-2,0).
∴直线l的解析式为y=2x,
∵点A(2,m)在直线l上,
∴m=2×2=4.
∴点A的坐标为(2,4),
又∵点A(2,4)在反比例函数y=
| k |
| x |
∴4=
| k |
| 2 |
∴k=8.
∴反比例函数的解析式为y=
| 8 |
| x |

(2)过A作AM⊥x轴于M,
∵A(2,4),
∴AM=4,OM=2,∠AMB=90°,
∴∠ABO=∠BAM=45°,
∴MB2=MB1=AM=4,
∴B2的坐标是(6,0),B1的坐标是(-2,0),
即B的坐标是(6,0)或(-2,0).
点评:本题考查了轴对称性质,用待定系数法求出反比例函数的解析式,等腰直角三角形性质的应用,主要考查学生的计算能力,题目是一道比较典型的题目,难度适中.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案
相关题目
 在一次远足活动中,小聪由甲地步行到乙地后原路返回;小明由甲地步行到乙地后也原路返回,但小明在返回途中走到丙地时发现物品可能遗忘在乙地,于是从丙返回乙地,然后沿原路返回.两人同时出发,步行过程中保持匀速.设步行的时间为t(h),两人离甲地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.
在一次远足活动中,小聪由甲地步行到乙地后原路返回;小明由甲地步行到乙地后也原路返回,但小明在返回途中走到丙地时发现物品可能遗忘在乙地,于是从丙返回乙地,然后沿原路返回.两人同时出发,步行过程中保持匀速.设步行的时间为t(h),两人离甲地的距离分别为S1(km)和S2(km),图中的折线分别表示S1、S2与t之间的函数关系.