题目内容
13.如图(1):△ABC中,∠B、∠C的平分线相交于点O,过点O作EF∥BC分别交AB、AC于E、F.(1)EF与BE、CF之间有什么关系?(不证明)
(2)若△ABC中,∠B的平分线与三角外角∠ACD的平分线CO交于点O,过点O作OE∥BC交AB于E,交AC于F(图示),EF与BE,CF之间又有怎样的数量关系,并给予证明.

分析 (1)根据角平分线定义和平行线性质求出∠EOB=∠EBO,推出OE=BE,同理得出CF=OF,即可求出答案.
(2)结合图形特点,根据(1)中规律,EF=BE-CF.
解答 解:(1)EF=BE+CF.
证明:∵BO平分∠ABC,
∴∠EBO=∠OBC,
∵EF∥BC,
∴∠EDB=∠OBC,
∴∠EOB=∠EBO,
∴OE=BE,
同理CF=OF,
∴EF=OE+OF=BE+CF,
即BE+CF=EF.
(2)EF=BE-CF.
证明:∵BO平分∠ABC,
∴∠EBO=∠CBO,
∴BE=OE,
同理:CF=OF,
∴EF=OE-OF=BE-CF.
点评 本题主要考查等腰三角形的判定和性质,结合平行得到BE=EO,CF=OF是解题的关键.

练习册系列答案
相关题目
4.洪峰到来前,120名战士奉命加固堤坝,已知5人运沙袋3人堆垒沙袋,正好运来的沙袋能及时用上且不窝工,为了合理安排,如果设x人运送沙袋,其余人堆垒沙袋,那么以下所列方程正确的是( )
| A. | $\frac{120-x}{2}$=x | B. | 120-x=$\frac{5}{3}$x | C. | x=$\frac{5}{3}$(120-x) | D. | 3x+2x=120 |
3.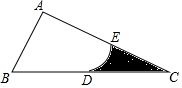 如图,在△ABC中,∠BAC=90°,BC=2AB=6,以点A为圆心,AB为半径作弧,分别交BC,AC于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠BAC=90°,BC=2AB=6,以点A为圆心,AB为半径作弧,分别交BC,AC于点D、E,则图中阴影部分的面积是( )
 如图,在△ABC中,∠BAC=90°,BC=2AB=6,以点A为圆心,AB为半径作弧,分别交BC,AC于点D、E,则图中阴影部分的面积是( )
如图,在△ABC中,∠BAC=90°,BC=2AB=6,以点A为圆心,AB为半径作弧,分别交BC,AC于点D、E,则图中阴影部分的面积是( )| A. | $\frac{9\sqrt{3}}{4}$-$\frac{3π}{2}$ | B. | $\frac{9\sqrt{2}}{4}$-$\frac{3π}{2}$ | C. | $\frac{9\sqrt{3}}{4}$-$\frac{3π}{4}$ | D. | $\frac{9\sqrt{2}}{4}$-$\frac{3π}{4}$ |

 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠A=50°,则∠DBC=15°.
如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠A=50°,则∠DBC=15°.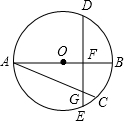 如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G.
如图,AB是⊙O的直径,AC是⊙O的弦,点D是$\widehat{ABC}$的中点,弦DE⊥AB,垂足为点F,DE交AC于点G.