题目内容
8. 如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠A=50°,则∠DBC=15°.
如图,在等腰三角形ABC中,AB=AC,DE垂直平分AB,已知∠A=50°,则∠DBC=15°.
分析 根据等边对等角,由已知的AB=AC得到∠ABC与∠C相等,由∠A的度数求出∠ABC的度数,然后由DE为AB的垂直平分线,根据线段垂直平分线的性质得到AD与BD相等,再根据等边对等角得到∠A与∠ABD相等,由∠ABC与∠ABD相减即可求出所求角的度数.
解答 解:∵AB=AC,且∠A=50°,
∴∠ABC=∠C=$\frac{180°-50°}{2}$=65°,
又∵DE是AB的垂直平分线,
∴AD=BD,
∴∠A=∠ABD=50°,
∴∠DBC=∠ABC-∠ABD=65°-50°=15°.
故答案为:15.
点评 此题考查了等腰三角形的性质,线段垂直平分线的性质.其中线段垂直平分线性质为线段垂直平分线上的点到线段两端点的距离相等.

练习册系列答案
相关题目
18.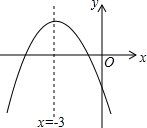 二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(-6,y2)是它图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(-6,y2)是它图象上的两点,则y1与y2的大小关系是( )
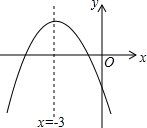 二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(-6,y2)是它图象上的两点,则y1与y2的大小关系是( )
二次函数y=ax2+bx+c的图象如图所示,若点A(1,y1)、B(-6,y2)是它图象上的两点,则y1与y2的大小关系是( )| A. | y1<y2 | B. | y1=y2 | C. | y1>y2 | D. | 不能确定 |

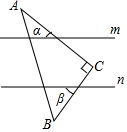 如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α、β,则α+β=90°.
如图,m∥n,直角三角板ABC的直角顶点C在两直线之间,两直角边与两直线相交所形成的锐角分别为α、β,则α+β=90°.