题目内容
10.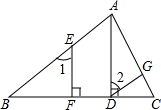 如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.
如图,已知AD⊥BC,EF⊥BC,∠1=∠2.求证:DG∥BA.证明:∵AD⊥BC,EF⊥BC (已知)
∴∠EFB=∠ADB=90°(垂直定义)
∴EF∥AD(同位角相等,两直线平行)
∴∠1=∠BAD(两直线平行,同位角相等)
又∵∠1=∠2 (已知)
∴∠2=∠BAD (等量代换)
∴DG∥BA.(内错角相等,两直线平行).
分析 根据垂直得出∠EFB=∠ADB=90°,根据平行线的判定得出EF∥AD,根据平行线的性质得出∠1=∠BAD,求出∠2=∠BAD,根据平行线的判定得出即可.
解答 证明:∵AD⊥BC,EF⊥BC (已知)
∴∠EFB=∠ADB=90°(垂直定义),
∴EF∥AD(同位角相等,两直线平行),
∴∠1=∠BAD(两直线平行,同位角相等),
又∵∠1=∠2 (已知),
∴∠2=∠BAD(等量代换),
∴DG∥BA(内错角相等,两直线平行),
故答案为:(垂直定义),同位角相等,两直线平行),(两直线平行,同位角相等),∠2=∠BAD,(
内错角相等,两直线平行).
点评 本题考查了平行线的性质和判定的应用,能灵活运用定理进行推理是解此题的关键.

练习册系列答案
相关题目
18.我校某美术小组的同学在毕业前夕,将自己三年来的写生作品向本组其他同学各赠送一件,全组共互赠送作品90件,如果设全组有x名同学,则可列方程为( )
| A. | x(x-1)=45 | B. | x(x+1)=45 | C. | x(x+1)=90 | D. | x(x-1)=90 |
 已知气温的华氏度数y是摄氏度数x的一次函数,如图所示是一个家用温度表的表盘,其左边为摄氏温度的刻度和度数(单位:℃),右边为华氏温度的刻度和度数(单位:℉),观察发现表示-40℃与-40℉的刻度线恰好对齐(左一条水平线上),而表示0℃与32℉的刻度线恰好对齐.
已知气温的华氏度数y是摄氏度数x的一次函数,如图所示是一个家用温度表的表盘,其左边为摄氏温度的刻度和度数(单位:℃),右边为华氏温度的刻度和度数(单位:℉),观察发现表示-40℃与-40℉的刻度线恰好对齐(左一条水平线上),而表示0℃与32℉的刻度线恰好对齐. 背景:某日,某国3艘炮艇迫袭5条中国渔船,刚刚完成黄岩岛护渔任务的“中国渔政310”船立即追往北纬11度22分、东经110度45分附近海域护渔.保护100多名中国渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.
背景:某日,某国3艘炮艇迫袭5条中国渔船,刚刚完成黄岩岛护渔任务的“中国渔政310”船立即追往北纬11度22分、东经110度45分附近海域护渔.保护100多名中国渔民免受财产损失和人身伤害.某国炮艇发现中国目前最先进的渔政船正在疾速驰救中国渔船,立即掉头离去.