题目内容

1．下列命题：（1）如果AC=BC，那么点C是线段AB的中点；（2）不相等的两个角一定不是对顶角；（3）直角三角形的两个锐角互余；（4）同位角相等；（5）两点之间直线最短．其中真命题的个数有（　　）
A．1个B．2个C．3个D．4个

分析 由等腰三角形的判定、对顶角的性质、直角三角形的性质、平行线的性质、线段的性质对各选项分别判断即可．

解答 解：（1）如果AC=BC，那么点C不一定是线段AB的中点；故（1）是假命题；
（2）不相等的两个角一定不是对顶角；故（2）是真命题；
（3）直角三角形的两个锐角互余；故（3）是真命题；
（4）两直线平行，同位角相等；故（4）是假命题；
（5）两点之间线段最短；故（5）是假命题；
真命题的个数有2个；故选：B．

点评 本题考查了命题与定理、等腰三角形的判定、对顶角相等的性质、直角三角形的性质、平行线的性质、相等的性质等知识；难度不大．

练习册系列答案
相关题目
11．如图，△ABC三个顶点的坐标分别是A（1，1），B（4，2），C（3，4）．
（1）请画出将△ABC先向左，再向下都平移5个单位长度后得到的△A1B1C1；
（2）请画出将△ABC绕O按逆时针方向旋转90°后得到的△A2B2C2；
（3）在x轴上求作一点P，使△PAB周长最小，请画出△PAB，并直接写出点P的坐标．
12．在△ABC中，以AB为斜边，作直角△ABD，使点D落在△ABC内，∠ADB=90°．

（1）如图1，若AB=AC，∠BAD=30°，AD=6$\sqrt{3}$，点P、M分别为BC、AB边的中点，连接PM，求线段PM的长；
（2）如图2，若AB=AC，把△ABD绕点A逆时针旋转一定角度，得到△ACE，连接ED并延长交BC于点P，求证：BP=CP
（3）如图3，若AD=BD，过点D的直线交AC于点E，交BC于点F，EF⊥AC，且AE=EC，请直接写出线段BF、FC、AD之间的关系（不需要证明）．
9．计算题
（1）（-17）+59+（-37）
（2）$\frac{5}{6}$+（-2$\frac{1}{2}$）-（-1$\frac{1}{6}$）-（+0.5）
（3）-（+0.5）-（-3$\frac{1}{4}$）+2.75-（+7$\frac{1}{2}$）
（4）3.75-（-$\frac{1}{2}$）+（-4$\frac{2}{3}$）+（0.5）+（-6$\frac{3}{4}$）
16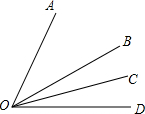．如图，OB平分∠AOD，OC平分∠BOD，∠AOC=45°，则∠BOC=（　　）
A．5°B．10°C．15°D．20°
6．下列函数关系式：（1）y=-x； （2）y=2x+11；  （3）y=x2； （4）$y=\frac{1}{x}$，其中一次函数的个数是（　　）
A．1B．2C．3D．4
13．如图，菱形ABCD的一边中点M到对角线交点O的距离为5cm，则菱形ABCD的周长为（　　）
A．5 cmB．10 cmC．20 cmD．40 cm
10．下列给出4个命题：
①内错角相等；
②对顶角相等；
③对于任意实数x，代数式x2-6x+10总是正数；
④若三条线段a、b、c满足a+b＞c，则三条线段a、b、c一定能组成三角形．
其中正确命题的个数是（　　）
A．1个B．2个C．3个D．4个
11． 如图OA⊥OB，若∠BOC=40°，则∠AOC的度数是（　　）
A．20°B．40°C．50°D．60°

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网