题目内容
5.已知菱形的四个顶点分别是A、B、C、D,顶点A(2,2)、D(4,-2)且点B在x轴上,点C在平面直角坐标系内,求顶点B、C的坐标.分析 有两种情形,先求出点B的坐标,再利用一次函数的有关知识,通过解方程组求出点C的坐标.
解答 解:由题意 ,线段AD只能是菱形的边,不可能为对角线,
,线段AD只能是菱形的边,不可能为对角线,
设点B(m,0),则∵AB=AD
∴(m-2)2+22=(4-2)2+(-2-2)2,
m=6或-2,
∴B1(-2,0),B2(6,0),
∵直线AD为y=-2x+6,AD∥B1C1
∴直线B1C1为y=-2x-4,
直线DC1为y=$\frac{1}{2}$x-4,
由$\left\{\begin{array}{l}{y=-2x-4}\\{y=\frac{1}{2}x-4}\end{array}\right.$解得$\left\{\begin{array}{l}{x=0}\\{y=-4}\end{array}\right.$,
∴点C1坐标为(0,-4).
∵直线B2C2为y=-2x+12,直线AB2为y=-$\frac{1}{2}$x+3,直线DC2为y=-$\frac{1}{2}$x,
由$\left\{\begin{array}{l}{y=-\frac{1}{2}x}\\{y=-2x+12}\end{array}\right.$解得$\left\{\begin{array}{l}{x=8}\\{y=-4}\end{array}\right.$,
∴点C2坐标为(8,-4).
∴B点坐标(-2,0)或(6,0),点C坐标(0,-4)或(8,-4).
点评 本题考查菱形的性质、一次函数、两点之间的距离公式等知识,解题的关键是构建一次函数,通过解方程组解决问题,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.下面各图象不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
13.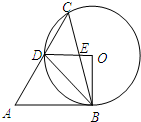 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )| A. | ∠BOD=90° | B. | DO∥AB | C. | CD=AD | D. | △BDE∽△BCD |
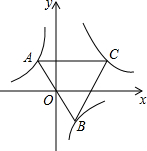 如图,已知点A是双曲线y=-$\frac{5}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是15.
如图,已知点A是双曲线y=-$\frac{5}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是15.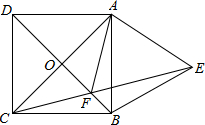 如图,已知正方形ABCD,以AB为边向外作等边三角形ABE,CE与DB相交于点F,则∠AFD的度数60°.
如图,已知正方形ABCD,以AB为边向外作等边三角形ABE,CE与DB相交于点F,则∠AFD的度数60°.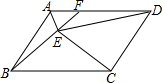 在图中,ABCD是平行四边形,F在AD上,△AEF的面积=8cm2,△DEF的面积=12cm2,四边形BCDF的面积=72cm2,求出△CDE的面积.
在图中,ABCD是平行四边形,F在AD上,△AEF的面积=8cm2,△DEF的面积=12cm2,四边形BCDF的面积=72cm2,求出△CDE的面积. 如图,二次函数y=-x2+bx+c的图象(抛物线)与x轴交于A(1,0),且当x=0和x=-2时所对应的函数值相等.
如图,二次函数y=-x2+bx+c的图象(抛物线)与x轴交于A(1,0),且当x=0和x=-2时所对应的函数值相等.