题目内容
20.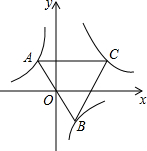 如图,已知点A是双曲线y=-$\frac{5}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是15.
如图,已知点A是双曲线y=-$\frac{5}{x}$在第二象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第一象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=$\frac{k}{x}$(k>0)上运动,则k的值是15.
分析 设点A的坐标为(a,-$\frac{5}{a}$),连接OC,则OC⊥AB,表示出OC,过点C作CD⊥x轴于点D,设出点C坐标,在Rt△OCD中,利用勾股定理可得出x2的值,继而得出y与x的函数关系式.
解答 解:设A(a,-$\frac{5}{a}$),
∵点A与点B关于原点对称,
∴OA=OB,
∵△ABC为等边三角形,
∴AB⊥OC,OC=$\sqrt{3}$AO,
∵AO=$\sqrt{{a}^{2}+(\frac{5}{a})^{2}}$,
∴CO=$\sqrt{3}$AO=$\sqrt{3{a}^{2}+\frac{75}{{a}^{2}}}$,
过点C作CD⊥x轴于点D,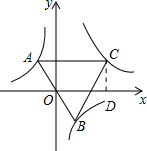
则可得∠BOD=∠OCD(都是∠COD的余角),
设点C的坐标为(x,y),则tan∠BOD=tan∠OCD,即$\frac{\frac{5}{a}}{a}$=$\frac{x}{y}$,
解得:y=$\frac{{a}^{2}}{5}$x,
在Rt△COD中,CD2+OD2=OC2,即y2+x2=3a2+$\frac{75}{{a}^{2}}$,
将y=$\frac{{a}^{2}}{5}$x代入,
可得:k=xy=15.
故答案为15.
点评 本题考查了反比例函数的综合题,涉及了解直角三角形、等边三角形的性质及勾股定理的知识,综合考察的知识点较多,解答本题的关键是将所学知识融会贯通,注意培养自己解答综合题的能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
8. 如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
 如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
10.清明节是中国传统节日,它不仅是人们远足踏青的日子,更是祭奠祖先、缅怀先人的节日.市民政局提供的数据显示,今年清明节当天全市213处祭扫点共接待群众264000人,将264000用科学记数法表示应为( )
| A. | 264×103 | B. | 2.64×104 | C. | 2.64×105 | D. | 0.264×106 |
 如图,将矩形纸ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E,若CD=6,AD=18,则BE=10.
如图,将矩形纸ABCD沿对角线BD折叠,使点A落在平面上的F点处,DF交BC于点E,若CD=6,AD=18,则BE=10.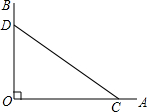 画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上.
画图、证明:如图,∠AOB=90°,点C、D分别在OA、OB上. 如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.
如图,△ABC内接于⊙O,若∠BAC=30°,BC=2,则⊙O的半径为2.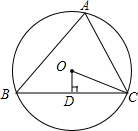 如图,△ABC内接于⊙O,OD⊥BC于点D,若∠A=70°,则∠COD的大小为70°(度).
如图,△ABC内接于⊙O,OD⊥BC于点D,若∠A=70°,则∠COD的大小为70°(度).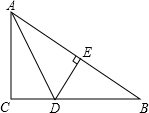 △ABC中,∠C=90°,AD为角平分线,BC=64,BD:DC=9:7,求D到AB的距离.
△ABC中,∠C=90°,AD为角平分线,BC=64,BD:DC=9:7,求D到AB的距离.