题目内容
13.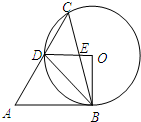 如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )
如图,在锐角△ABC中,∠A=60°,∠ACB=45°,以BC为弦作⊙O,交AC于点D,OD与BC交于点E,若AB与⊙O相切,则下列结论错误的是( )| A. | ∠BOD=90° | B. | DO∥AB | C. | CD=AD | D. | △BDE∽△BCD |
分析 根据圆周角定理对A进行判断;根据切线的性质得到OB⊥AB,然后根据平行线的判断方法对B进行判断;利用点C为动点可对C进行判断;根据相似三角形的判定方法对D进行判断.
解答 解:A、∠BOD=2∠BCD=90°,所以A选项的结论正确;
B、因为AB与⊙O相切,则OB⊥AB,而∠BOD=90°,则DO∥AB,所以B选项的结论正确;
C、因为点C为优弧BD上一点,C点靠近点D时,CD≠AD,所以C选项的结论错误;
D、因为∠BOD=90°,OB=OD,则∠ODB=45°,所以∠ODB=∠C,而∠DBE=∠CBD,所以△BDE∽△BCD,所以D选项的结论正确.
故选C.
点评 本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理和相似三角形的判定.

练习册系列答案
相关题目
3.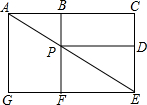 如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
 如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )
如图、一只小虫子欲从A点不重复的经过图中的每一个点或每一条线段而最终到达目的地E,试问这只小虫子沿A→P→E行走的概率是( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{9}$ | D. | $\frac{1}{12}$ |
1.下列各组中的两项,不是同类项的是( )
| A. | 23与32 | B. | m2n与$-\frac{1}{2}m{n^2}$ | C. | 2πR与π2R | D. | -x2y与2yx2 |
8. 如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
 如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )
如图,PA、PB是⊙O的切线,AC是⊙O直径,∠c=55°,则∠APB等于( )| A. | 55° | B. | 60° | C. | 65° | D. | 70° |
18.下列各曲线中不能表示y是x的函数的是( )
| A. |  | B. |  | C. |  | D. |  |
2.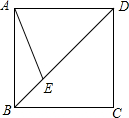 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
 如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,则BE的长为( )| A. | $\sqrt{2}$ | B. | 2 | C. | 4$\sqrt{2}$-4 | D. | 4-2$\sqrt{2}$ |
3.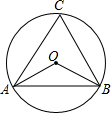 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
 如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )
如图,△ABC内接于⊙O,若∠AOB=110°,则∠ACB的度数是( )| A. | 70° | B. | 60° | C. | 55° | D. | 50° |
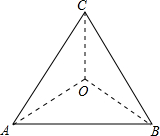 如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.
如图,边长为3的等边△ABC内一点O到三个顶点的距离都相等,则OA=$\sqrt{3}$.