题目内容
19. 如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
分析 先过C作CM⊥BA,交BA是延长线于M,过G作GN⊥FE,交FE的延长线于N,根据Rt△ACM中,AM=$\frac{1}{2}$AC=1米,CM=$\sqrt{3}$米,可得EC+CM=2+$\sqrt{3}$≈3.7米,再根据Rt△EGN中,GN=$\frac{\sqrt{2}}{2}$EG=$\frac{\sqrt{2}}{2}$米,可得GN+EC=$\frac{\sqrt{2}}{2}$+2≈2.7米,据此可得路灯F到公路AB、路灯G到公路CD的距离.
解答 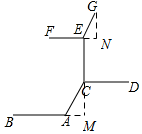 解:如图所示,过C作CM⊥BA,交BA是延长线于M,过G作GN⊥FE,交FE的延长线于N,
解:如图所示,过C作CM⊥BA,交BA是延长线于M,过G作GN⊥FE,交FE的延长线于N,
∵AC=CE=2米,∠BAC=120°,
∴∠CAM=60°,∠ACM=30°,
∴Rt△ACM中,AM=$\frac{1}{2}$AC=1米,CM=$\sqrt{3}$米,
∴EC+CM=2+$\sqrt{3}$≈3.7米,
∵EF∥AB∥CD,CE⊥CD,
∴路灯F到公路AB的距离为3.7米;
∵∠FEG=135°,
∴∠GEN=45°,
∴Rt△EGN中,GN=$\frac{\sqrt{2}}{2}$EG=$\frac{\sqrt{2}}{2}$米,
∴GN+EC=$\frac{\sqrt{2}}{2}$+2≈2.7米,
∵EF∥AB∥CD,CE⊥CD,
∴路灯G到公路CD的距离为2.7米.
点评 本题主要考查了解直角三角形的应用,在解决坡度的有关问题中,一般通过作高构成直角三角形,坡角即是一锐角,坡度实际就是一锐角的正切值,水平宽度或铅直高度都是直角边,实质也是解直角三角形问题.

练习册系列答案
相关题目
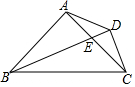 在△ABC中,AB=AC,∠BAC=90°,点E在AC边上,BE平分∠ABC,CD⊥BE于点D,连接AD,若BE=10,则AD的长是5.
在△ABC中,AB=AC,∠BAC=90°,点E在AC边上,BE平分∠ABC,CD⊥BE于点D,连接AD,若BE=10,则AD的长是5.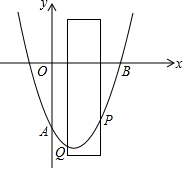 如图,已知抛物线y=ax2-2x-8(a>0)交y轴于点A,与x轴的正半轴交于点B,有一宽度为2的直尺平行于y轴,在点A、B之间平行移动,直尺的两长边所在的直线与抛物线分别交于P、Q两点,P、Q两点的纵坐标分别用yP和yQ表示,设点Q的横坐标为m(m≥0),若yP-yQ的最小值为2,则实数a的值为$\frac{3}{2}$.
如图,已知抛物线y=ax2-2x-8(a>0)交y轴于点A,与x轴的正半轴交于点B,有一宽度为2的直尺平行于y轴,在点A、B之间平行移动,直尺的两长边所在的直线与抛物线分别交于P、Q两点,P、Q两点的纵坐标分别用yP和yQ表示,设点Q的横坐标为m(m≥0),若yP-yQ的最小值为2,则实数a的值为$\frac{3}{2}$.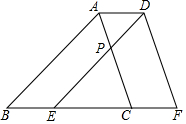 如图,已知点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.
如图,已知点E,C在线段BF上,BE=CF,∠B=∠DEF,∠ACB=∠F,求证:四边形ABED为平行四边形.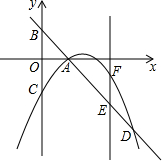 如图,在平面直角坐标中,直线y=-x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx-2与y轴交于点C,与直线AB的另一个交点为D,点E是射线BA上一点(不与点A、B重合),点F在抛物线上,且EF∥y轴,设点E的横坐标为m.
如图,在平面直角坐标中,直线y=-x+2交x轴于点A,交y轴于点B,过点A的抛物线y=ax2+bx-2与y轴交于点C,与直线AB的另一个交点为D,点E是射线BA上一点(不与点A、B重合),点F在抛物线上,且EF∥y轴,设点E的横坐标为m.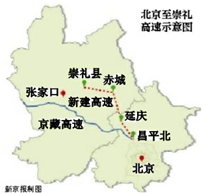 为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?
为保障北京2022 年冬季奥运会赛场间的交通服务,北京将建设连接北京城区-延庆区-崇礼县三地的高速铁路和高速公路.在高速公路方面,目前主要的交通方式是通过京藏高速公路(G6),其路程为220公里.为将崇礼县纳入北京一小时交通圈,有望新建一条高速公路,将北京城区到崇礼的道路长度缩短到100公里.如果行驶的平均速度每小时比原来快22公里,那么从新建高速行驶全程所需时间与从原高速行驶全程所需时间比为4:11.求从新建高速公路行驶全程需要多少小时?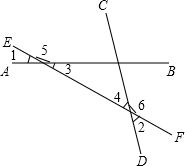 如图所示,直线AB、CD、EF两两相交,若∠1=30°,∠2=60°,则∠3=30°,∠4=60°,∠5=150°,∠6=120°.
如图所示,直线AB、CD、EF两两相交,若∠1=30°,∠2=60°,则∠3=30°,∠4=60°,∠5=150°,∠6=120°. 如图所示,点B,E,F,C在同一条直线上,AF⊥BC于F,DE⊥BC于E,AB∥CD,BE=CF,求证:AB=DC.
如图所示,点B,E,F,C在同一条直线上,AF⊥BC于F,DE⊥BC于E,AB∥CD,BE=CF,求证:AB=DC.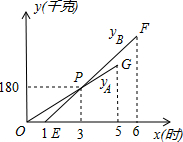 某物流公司引进A、B两种机器人用来搬运某种货物.这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题:
某物流公司引进A、B两种机器人用来搬运某种货物.这两种机器人充满电后可以连续搬运5小时,A种机器人于某日0时开始搬运,过了1小时,B种机器人也开始搬运,如图,线段OG表示A种机器人的搬运量yA(千克)与时间x(时)的函数图象,线段EF表示B种机器人的搬运量yB(千克)与时间x(时)的函数图象,根据图象提供的信息,解答下列问题: