题目内容
10.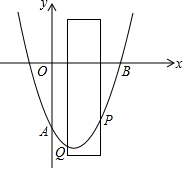 如图,已知抛物线y=ax2-2x-8(a>0)交y轴于点A,与x轴的正半轴交于点B,有一宽度为2的直尺平行于y轴,在点A、B之间平行移动,直尺的两长边所在的直线与抛物线分别交于P、Q两点,P、Q两点的纵坐标分别用yP和yQ表示,设点Q的横坐标为m(m≥0),若yP-yQ的最小值为2,则实数a的值为$\frac{3}{2}$.
如图,已知抛物线y=ax2-2x-8(a>0)交y轴于点A,与x轴的正半轴交于点B,有一宽度为2的直尺平行于y轴,在点A、B之间平行移动,直尺的两长边所在的直线与抛物线分别交于P、Q两点,P、Q两点的纵坐标分别用yP和yQ表示,设点Q的横坐标为m(m≥0),若yP-yQ的最小值为2,则实数a的值为$\frac{3}{2}$.
分析 由题意可得,点Q的坐标为(m,am2-2m-8),点P的坐标为(m+2,a(m+2)2-2(m+2)-8),得到yP-yQ=4am+4a-4,由a>0,于是得到yP-yQ轴随m的减小而减小,于是得到结论.
解答 解:由题意可得,
点Q的坐标为(m,am2-2m-8),点P的坐标为(m+2,a(m+2)2-2(m+2)-8),
∴yP-yQ
=a(m+2)2-2(m+2)-8-[am2-2m-8]
=4am+4a-4,∵a>0,∴yP-yQ轴随m的减小而减小,∵m≥0,∴m的最小值是0,
即m=0时,yP-yQ=4am+4a-4=2,解得:a=$\frac{3}{2}$,
故答案为:$\frac{3}{2}$.
点评 本题考查了抛物线与x轴的交点,二次函数图象上点的坐标特征,坐标与图形性质,正确的理解题意是解题的关键.

练习册系列答案
相关题目
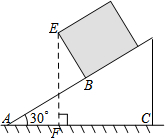 一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m.
一个长方体木箱沿斜面下滑,当木箱滑至如图位置时,AB=3m,己知木箱高BE=$\sqrt{3}$m,斜面坡角为30°,则木箱端点E距地面AC的高度为3m. 如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).