题目内容
9.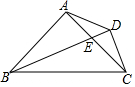 在△ABC中,AB=AC,∠BAC=90°,点E在AC边上,BE平分∠ABC,CD⊥BE于点D,连接AD,若BE=10,则AD的长是5.
在△ABC中,AB=AC,∠BAC=90°,点E在AC边上,BE平分∠ABC,CD⊥BE于点D,连接AD,若BE=10,则AD的长是5.
分析 延长BA、CD相交于点F,根据同角的余角相等求出∠F=∠AEB,再利用“角角边”求出△ABE和△ACF全等,根据全等三角形对应边相等可得CF=BE,再利用“角边角”证明△BCD和△BFD全等,根据全等三角形对应边相等可得CD=DF,最后根据直角三角形斜边上的中线等于斜边的一半可得AD=$\frac{1}{2}$CF.
解答 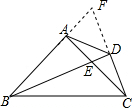 解:如图,延长BA、CD相交于点F,
解:如图,延长BA、CD相交于点F,
∵∠BAC=90°,CD⊥BE,
∴∠ABE+∠AEB=90°,
∠ABE+∠F=90°,
∴∠F=∠AEB,
在△ABE和△ACF中,$\left\{\begin{array}{l}{∠F=∠AEB}\\{∠BAE=∠CAF=90°}\\{AB=AC}\end{array}\right.$,
∴△ABE≌△ACF(AAS),
∴CF=BE=10,
∵BE平分∠ABC,
∴∠BCD=∠DBF,
在△BCD和△BFD中,$\left\{\begin{array}{l}{∠BCD=∠DBF}\\{BD=BD}\\{∠BDC=∠BDF=90°}\end{array}\right.$,
∴△BCD≌△BFD(ASA),
∴CD=DF,
又∵∠CAF=∠BAC=90°,
∴AD=$\frac{1}{2}$CF=$\frac{1}{2}$×10=5.
故答案为:5.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的性质,直角三角形斜边上的中线等于斜边的一半的性质,熟练掌握三角形全等的判定方法并作辅助线构造出全等三角形是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
17.某加工厂以每吨3000元的价格购进50吨原料进行加工.若进行粗加工,每吨加工费用为600元,需$\frac{1}{3}$天,每吨售价4000元;若进行精加工,每吨加工费用为900元,需$\frac{1}{2}$天,每吨售价4500元.现将这50吨原料全部加工完.设其中粗加工x吨,获利y元.
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
表二
(2)如果必须在20天内完成,如何安排生产才能获得最大利润,最大利润是多少?
(1)请完成表格并求出y与x的函数关系式(不要求写自变量的范围);
表一
| 粗加工数量/吨 | 3 | 7 | x |
| 精加工数量/吨 | 47 | 43 | 50-x |
| 粗加工数量/吨 | 3 | 7 | x |
| 粗加工获利/元 | 1200 | 2800 | 400x |
| 精加工获利/元 | 28200 | 25800 | 600(50-x) |
4.$\frac{14}{3}$是( )
| A. | 整数 | B. | 无理数 | C. | 有理数 | D. | 自然数 |
 如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).
如图,两条平行的公路AB与CD之间有一个斜坡AC,在C处垂直树立着一个路灯CE,灯杆CE上有两根灯臂EF和EG,两灯臂上的路灯F、G分别照明AB、CD两条公路.已知AC=CE=2米,EG=1米,∠BAC=120°,∠FEG=135°.EF∥AB,分别求路灯F到公路AB、路灯G到公路CD的距离(结果精确到0.1米.参考数据:$\sqrt{3}$≈1.73,$\sqrt{2}$≈1.41).