题目内容
已知a、b、c均为实数,且a+b+c=0,abc=2,求|a|+|b|+|c|的最小值.
考点:根的判别式
专题:综合题
分析:由a+b+c=0,abc=2,得到a,b,c中有两个负数,一个正数,不妨设a<0,b<0,c>0,再由a+b=-c,ab=
,这样可以把a,b看作方程x2+cx+
=0,根据根的判别式得到△=c2-4•
≥0,解得c≥2,然后化简原式得到-a-b+c=2c,即可得到|a|+|b|+|c|的最小值.
| 2 |
| c |
| 2 |
| c |
| 2 |
| c |
解答:解:∵a+b+c=0,abc=2,
∴a,b,c中有两个负数,一个正数,
不妨设a<0,b<0,c>0,
∴a+b=-c,ab=
,
∴可以把a,b看作方程x2+cx+
=0的解,
∴△=c2-4•
≥0,解得c≥2,
∴原式=-a-b+c=2c≥4,
即|a|+|b|+|c|的最小值为4.
∴a,b,c中有两个负数,一个正数,
不妨设a<0,b<0,c>0,
∴a+b=-c,ab=
| 2 |
| c |
∴可以把a,b看作方程x2+cx+
| 2 |
| c |
∴△=c2-4•
| 2 |
| c |
∴原式=-a-b+c=2c≥4,
即|a|+|b|+|c|的最小值为4.
点评:本题考查了一元二次方程根的判别式:如方程有两个实数根,则△≥0.也考查了一元二次方程根与系数的关系以及绝对值的含义.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
礼堂第一排有a个座位,后面每排多1个座位,礼堂共有15排座位,则这礼堂的座位总数有( )个.
| A、15a+105 |
| B、15a+136 |
| C、15a+120 |
| D、14a+105 |
下列式子中的各字母均为实数,其中不可能成立的式子是( )
| A、(a-b)2=a2-b2 | ||
| B、x3+x2=x5 | ||
| C、x-1=-x | ||
D、
|
若ab≠1,且有a2+2010a+6=0及6b2+2010b+1=0,则
的值是( )
| a |
| b |
| A、6 | ||
B、
| ||
| C、2010 | ||
D、
|
已知
+
=
,
+
=
,
+
=
,则
+
+
的值为( )
| 1 |
| x |
| 1 |
| y+z |
| 1 |
| 2 |
| 1 |
| y |
| 1 |
| z+x |
| 1 |
| 3 |
| 1 |
| z |
| 1 |
| x+y |
| 1 |
| 4 |
| 2 |
| x |
| 3 |
| y |
| 4 |
| z |
| A、1 | ||
B、
| ||
| C、2 | ||
D、
|
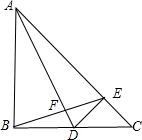 已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.
已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.