题目内容
方程|x-|2x-1||=3的解是
.
考点:含绝对值符号的一元一次方程
专题:计算题
分析:本题就①x≥
时,②x<
两种情况讨论.再就所求的结果验证其合理性.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:①当x≥
时,则|x-|2x-1||=3,
?|x-2x+1|=3,
?|x-1|=3,
?x-1=3或x-1=-3,
解得x=4或x=-2(不合题意舍去)
②当x<
时,则|x-|2x-1||=3,
?|x-1+2x|=3,
?|3x-1|=3,
?3x-1=3或3x-1=-3,
解得x=
(不合题意舍去)或x=-
,
综上所述方程|x-|2x-1||=3的解是:4或-
.
故答案为:4或-
.
| 1 |
| 2 |
?|x-2x+1|=3,
?|x-1|=3,
?x-1=3或x-1=-3,
解得x=4或x=-2(不合题意舍去)
②当x<
| 1 |
| 2 |
?|x-1+2x|=3,
?|3x-1|=3,
?3x-1=3或3x-1=-3,
解得x=
| 4 |
| 3 |
| 2 |
| 3 |
综上所述方程|x-|2x-1||=3的解是:4或-
| 2 |
| 3 |
故答案为:4或-
| 2 |
| 3 |
点评:本题考查含绝对值符号的一元一次方程的解法.解决本题的关键是区分好x取值范围,从而合理去掉绝对值符号,并就方程的解验证其合理性.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
 如图,⊙O的直径为8cm,弦CD垂直平分半径OA,则弦CD的长为( )
如图,⊙O的直径为8cm,弦CD垂直平分半径OA,则弦CD的长为( )| A、3cm | ||
B、2
| ||
C、4
| ||
D、8
|
已知实数x满足条件x>
x+1,那么
+
的值等于( )
| 2 |
| (x+2)2 |
| 3 | (x-3)3 |
| A、2x-1 | B、-2x+1 |
| C、-5 | D、1 |
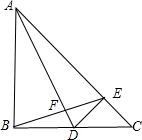 已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.
已知如图,△ABC中,∠ABC=90°,AB=BC,D是BC边上一点,DE⊥AC于E,连BE交AD与F.