题目内容
19.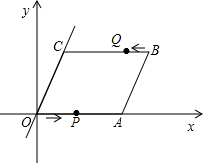 如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,4$\sqrt{3}$)
如图,在直角坐标系中,点O是坐标原点,四边形OABC是平行四边形,点A的坐标为(14,0),点B的坐标为(18,4$\sqrt{3}$)(1)写出点C的坐标(4,4$\sqrt{3}$)
(2)动点P从O出发,沿射线OA方向以每秒2个单位的速度运动,点Q从B出发以每秒1个单位的速度向点C运动,它们同时出发,当点Q到达点C时另一点也停止运动,设运动时间为t秒,求t为何值时,以P、Q、A、B为顶点的四边形是平行四边形.
分析 (1)延长BC交y轴于点D,则可求得BD,结合平行四边形的性质可求得BC=OA,可求得CD,且BC∥OA,可求得C点坐标;
(2)分两种情况,当P点在线段OA上时,此时有AP∥BQ,且AP=BQ,可求得t的值;当P点在OA的延长线上时,此时由BQ=PA,可求得t的值.
解答 解:
(1)延长BC交y轴于点D,如图1,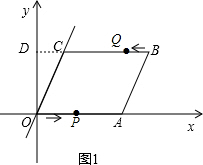
∵四边形OABC为平行四边形,
∴BC∥OA,且BC=OA,
∵A(14,0),B(18,4$\sqrt{3}$),
∴BC=OA=14,BD=18,OD=4$\sqrt{3}$,
∴CD=BD-BC=18-14=4,
∴C点坐标为(4,4$\sqrt{3}$),
故答案为:(4,4$\sqrt{3}$);
(2)当点P在线段OA上时,如图2,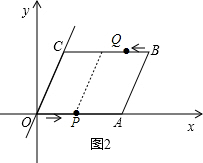
∵BC=14,
∴0≤t≤14
由题意可知OP=2t,BQ=t,
又OA=14,
∴AP=OA-OP=14-2t,
当四边形ABPQ为平行四边形时,则有AP=BQ,即14-2t=t,
解得t=$\frac{14}{3}$;
当点P在线段OA的延长线上时,如图3,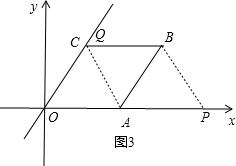
同上可知OP=2t,OA=14,BQ=t,
∴AP=OP-OA=2t-14,
∵四边形APBQ为平行四边形,
∴AP=BQ,即2t-14=t,
解得t=14,即Q与C点重合时,
综上可知当t为$\frac{14}{3}$或14时,以P、Q、A、B为顶点的四边形是平行四边形.
点评 本题主要考查平行四边形的性质和判定及点的坐标等知识点.掌握平行四边形的对边平行且相等是解题的关键,在(2)中注意按P点的位置分两种情况讨论.本题知识点不多,难度不大,属于基础题.化“动为静”是解决运动类问题的基本思路,即用t表示出线段的长度,从而得到关于t的方程求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.如果不等式组$\left\{\begin{array}{l}{x+2a≥4}\\{\frac{2x-b}{3}<1}\end{array}\right.$的解集是0≤x<1,那么a+b的值为1.
6.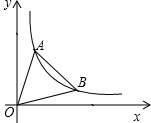 如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
 如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )
如图,A(x1,y1)B(x2,y2)是反比例函数y=$\frac{1}{x}$(x>0)的图象上的两点,且y1+y2=$\frac{7}{2}$,x2-x1=$\frac{5}{3}$,则△AOB的面积为( )| A. | 2$\frac{10}{11}$ | B. | 2$\frac{11}{12}$ | C. | 2$\frac{12}{13}$ | D. | 2$\frac{13}{14}$ |