题目内容
15.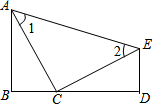 已知,如图,B、C、D三点共线,AB⊥BD,ED⊥CD,C是BD上的一点,且AB=CD,∠1=∠2,请判断△ACE的形状并说明理由.
已知,如图,B、C、D三点共线,AB⊥BD,ED⊥CD,C是BD上的一点,且AB=CD,∠1=∠2,请判断△ACE的形状并说明理由.
分析 由∠1=∠2可得AC=CE,再加上AB=CD,AB⊥BD,ED⊥CD,可直接证明三角形ABC与三角形CDE全等,从而易得三角形ACE是等腰直角三角形.
解答 解:∵∠1=∠2,
∴AC=CE,
∵AB⊥BD,ED⊥CD,
在△ABC与△CDE中,
$\left\{\begin{array}{l}{AC=CE}\\{AB=CD}\end{array}\right.$,
∴△ABC≌△CDE,
∴∠ACB=∠CED,
∵∠CED+∠ECD=90°,
∴∠ACD+∠ECD=90°,
∴∠ACE=90°,
∴△ACE是等腰直角三角形.
点评 本题主要考查了“HL”定理的应用,全等三角形的性质,等腰直角三角形的判定与性质,属于基础题.

练习册系列答案
相关题目
20.一个蓄水池有15m3的水,以每分钟0.5m3的速度向池中注水,蓄水池中的水量Q(m3)与注水时间t(分)间的函数表达式为( )
| A. | Q=0.5t | B. | Q=15t | C. | Q=15+0.5t | D. | Q=15-0.5t |
4.若规定sin(α-β)=sinαcosβ-cosαsinβ,则sin15°=( )
| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |
5.对于二次函数y=x2-4x+7的图象,下列说法正确的是( )
| A. | 开口向下 | B. | 对称轴是x=-2 | C. | 顶点坐标是(2,3) | D. | 与x轴有两个交点 |
 如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又已知△ABC≌△A′CB,则∠BCA′:∠BB′C=5:2.
如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又已知△ABC≌△A′CB,则∠BCA′:∠BB′C=5:2.
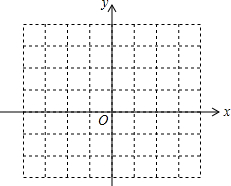 在平面直角坐标系中有一正方形网格,毎个小正方形的边长均为1,四边形各顶 点的坐标分别为A(1,1),B(3,1),C(3,2),D(2,3).
在平面直角坐标系中有一正方形网格,毎个小正方形的边长均为1,四边形各顶 点的坐标分别为A(1,1),B(3,1),C(3,2),D(2,3).