题目内容
5. 如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又已知△ABC≌△A′CB,则∠BCA′:∠BB′C=5:2.
如图,在△ABC中,∠A:∠ABC:∠ACB=3:5:10,又已知△ABC≌△A′CB,则∠BCA′:∠BB′C=5:2.
分析 先求出△ABC的各角的度数,再根据全等三角形对应角相等求出∠A′CB′的度数,利用三角形的外角知识求出∠BCB′和∠B′的度数,然后求出比值.
解答 解:∵∠A:∠ABC:∠ACB=3:5:10,
∴∠ACB=180°×$\frac{10}{3+5+10}$=100°,∠A=30°,∠ABC=180°-30°-100°=50°,
∵△A′B′C≌△ABC,
∴∠A′=∠A=30°,∠BCA′=∠ABC=50°,
∴∠CBB′=∠A′+∠BCA=30°+50°=80°,
∵∠BCA=∠B′+∠B′BC,
∴∠B′=20°,
∴∠BCA′:∠BB′C=50°:20°=5:2.
故答案为5:2.
点评 本题主要考查全等三角形对应角相等的性质和三角形外角的知识,根据比值和三角形内角和定理求出∠ACB的度数是解题的关键.

练习册系列答案
相关题目
15.下面四省电视台标示图案中,属于轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
10.下列命题的逆命题正确的是( )
| A. | 对顶角相等 | |
| B. | 三边相等的三角形是等边三角形 | |
| C. | 如果一个四边形是正方形,那么它的四条边相等 | |
| D. | 如果一个四边形是矩形,那么它的对角线相等 |
14.某校对各个班级教室卫生情况的考评包括以下几项:门窗,桌椅,地面,一天,两个班级的各项卫生成绩分别如表:(单位:分)
(1)两个班的平均得分分别是多少;
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这三项得分依次按25%、35%、40%的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
| 门窗 | 桌椅 | 地面 | |
| 一班 | 85 | 90 | 95 |
| 二班 | 95 | 85 | 90 |
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这三项得分依次按25%、35%、40%的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
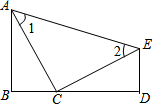 已知,如图,B、C、D三点共线,AB⊥BD,ED⊥CD,C是BD上的一点,且AB=CD,∠1=∠2,请判断△ACE的形状并说明理由.
已知,如图,B、C、D三点共线,AB⊥BD,ED⊥CD,C是BD上的一点,且AB=CD,∠1=∠2,请判断△ACE的形状并说明理由.