题目内容
4.若规定sin(α-β)=sinαcosβ-cosαsinβ,则sin15°=( )| A. | $\frac{\sqrt{2}-1}{2}$ | B. | $\frac{\sqrt{2}-\sqrt{6}}{4}$ | C. | $\frac{\sqrt{3}-1}{2}$ | D. | $\frac{\sqrt{6}-\sqrt{2}}{4}$ |
分析 根据题意把15°化为45°-30°,代入特殊角的三角函数值计算即可.
解答 解:由题意得,sin15°=sin(45°-30°)
=sin45°cos30°-cos45°sin30°
=$\frac{\sqrt{2}}{2}$×$\frac{\sqrt{3}}{2}$-$\frac{\sqrt{2}}{2}$×$\frac{1}{2}$
=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
故选:D.
点评 本题考查的是特殊角的三角函数值以及新定义,熟记特殊角的三角函数值是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.某校对各个班级教室卫生情况的考评包括以下几项:门窗,桌椅,地面,一天,两个班级的各项卫生成绩分别如表:(单位:分)
(1)两个班的平均得分分别是多少;
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这三项得分依次按25%、35%、40%的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
| 门窗 | 桌椅 | 地面 | |
| 一班 | 85 | 90 | 95 |
| 二班 | 95 | 85 | 90 |
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这三项得分依次按25%、35%、40%的比例计算各班的卫生成绩,那么哪个班的卫生成绩高?请说明理由.
13.下列说法正确的是( )
| A. | 掷一枚均匀的骰子,骰子停止转动后,6点朝上是必然事件 | |
| B. | 甲、乙两人在相同条件下各射击10次,他们的成绩平均数相同,方差是S2甲=0.4 | |
| C. | “明天降雨的概率为$\frac{1}{2}$”,表示明天有半天都在降雨 | |
| D. | 了解一批电视机的使用寿命,适合用普查的方式 |
14.徐州市总投资为44亿元的东三环路高架快速路建成,不仅疏解了中心城区的交通,还形成了我市的快速路网,拉动了个区域间的交流,44亿用科学记数法表示为( )
| A. | 0.44×109 | B. | 4.4×109 | C. | 44×108 | D. | 4.4×108 |
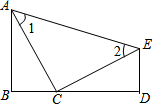 已知,如图,B、C、D三点共线,AB⊥BD,ED⊥CD,C是BD上的一点,且AB=CD,∠1=∠2,请判断△ACE的形状并说明理由.
已知,如图,B、C、D三点共线,AB⊥BD,ED⊥CD,C是BD上的一点,且AB=CD,∠1=∠2,请判断△ACE的形状并说明理由.