题目内容
18．
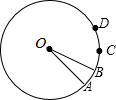如图，圆心角∠AOB=20°，将$\widehat{AB}$旋转n°得到$\widehat{CD}$，则$\widehat{CD}$的度数是20度．
分析 先根据旋转的性质得$\widehat{AB}$=$\widehat{CD}$，则根据圆心角、弧、弦的关系得到∠DOC=∠AOB=20°，然后根据圆心角的度数等于它所对弧的度数即可得到$\widehat{CD}$的度数．
解答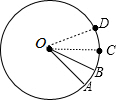 
解：∵将$\widehat{AB}$旋转n°得到$\widehat{CD}$，
∴$\widehat{AB}$=$\widehat{CD}$，
∴∠DOC=∠AOB=20°，
∴$\widehat{CD}$的度数为20度．
故答案为20．
点评 本题考查了圆心角、弧、弦的关系：在同圆或等圆中，如果两个圆心角、两条弧、两条弦中有一组量相等，那么它们所对应的其余各组量都分别相等．也考查了旋转的性质．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
13．分式-$\frac{1}{1-x}$可变形为（ ）
| A． | -$\frac{1}{x-1}$ | B． | $\frac{1}{1+x}$ | C． | -$\frac{1}{1+x}$ | D． | $\frac{1}{x-1}$ |
2．
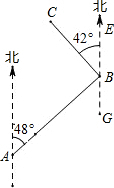如图，在A、B 两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（ ）
如图，在A、B 两地之间要修一条笔直的公路，从A地测得公路走向是北偏东48°，A，B两地同时开工，若干天后公路准确接通，若公路AB长8千米，另一条公路BC长是6千米，且BC的走向是北偏西42°，则A地到公路BC的距离是（ ）| A． | 6千米 | B． | 8千米 | C． | 10千米 | D． | 14千米 |
9．已知x2-5xy+6y2=0，则x：y等于（ ）
| A． | $\frac{1}{3}$或$\frac{1}{2}$ | B． | 2或3 | C． | $\frac{1}{6}$或1 | D． | 6或1 |
6．根据下面表格中的取值，方程x2+x-3=0有一个根的近似值（精确到0.1）是（ ）
| x | 1.2 | 1.3 | 1.4 | 1.5 |
| x2+x-3 | -0.36 | -0.01 | 0.36 | 0.75 |
| A． | 1.5 | B． | 1.2 | C． | 1.3 | D． | 1.4 |