题目内容
8.在一个边长为4的等边三角形纸片中,截出一个面积最大的矩形,并用该矩形围成一个圆柱形无底纸筒,则该纸筒的高为多少?分析 根据题意设BM=x,则DM=$\sqrt{3}$x,BD=2x,表示出矩形DMNE的面积,利用二次函数最值求法,进而得出答案.
解答 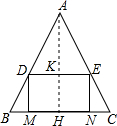 解:如图所示:过点A作AH⊥BC于点H,交DE于点K,
解:如图所示:过点A作AH⊥BC于点H,交DE于点K,
由题意可知:DE∥BC,
∵△ABC是等边三角形,
∴△ADE也是等边三角形,且∠BAH=30°,
∵AB=4cm,
∴AH=2$\sqrt{3}$cm,
设BM=x,则DM=$\sqrt{3}$x,BD=2x,
则AD=DE=4-2x,
S矩形DMNE=DM×DE=$\sqrt{3}$x(4-2x)=-2$\sqrt{3}$x2+4$\sqrt{3}$x,
当x=-$\frac{b}{2a}$=-$\frac{4\sqrt{3}}{2×(-2\sqrt{3})}$=1时,S最大,
即DM=$\sqrt{3}$cm,
则该纸筒的高为$\sqrt{3}$cm.
点评 此题主要考查了等边三角形的性质以及二次函数的应用,表示出矩形DMNE的面积是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
17.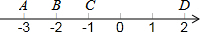 如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
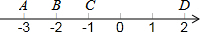 如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
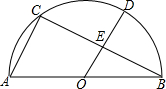 如图,已知点C,D是半圆$\widehat{AB}$上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论:
如图,已知点C,D是半圆$\widehat{AB}$上的三等分点,连接AC,BC,CD,OD,BC和OD相交于点E.则下列结论: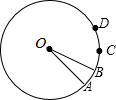 如图,圆心角∠AOB=20°,将$\widehat{AB}$旋转n°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20度.
如图,圆心角∠AOB=20°,将$\widehat{AB}$旋转n°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20度.