题目内容
6.已知△ABC∽△DEF,若△ABC与△DEF的相似比为2:3,则△ABC与△DEF对应边上中线的比为2:3.分析 相似三角形对应边上中线的比等于相似比,根据以上性质得出即可.
解答 解:∵△ABC∽△DEF,△ABC与△DEF的相似比为2:3,
∴△ABC与△DEF对应边上中线的比是2:3,
故答案为:2:3.
点评 本题考查了相似三角形的性质的应用,能理解相似三角形的性质是解此题的关键,注意:相似三角形对应边上中线的比等于相似比.

练习册系列答案
相关题目
17.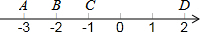 如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
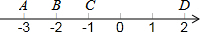 如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )
如图,数轴上的A、B、C、D四点中,与数-$\sqrt{3}$表示的点最接近的是( )| A. | 点A | B. | 点B | C. | 点C | D. | 点D |
1.计算3$\sqrt{2}$-$\sqrt{2}$的值是( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | 2$\sqrt{2}$ |
11.在数-3,-2,0,3中,大小在-1和2之间的数是( )
| A. | -3 | B. | -2 | C. | 0 | D. | 3 |
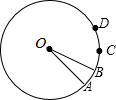 如图,圆心角∠AOB=20°,将$\widehat{AB}$旋转n°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20度.
如图,圆心角∠AOB=20°,将$\widehat{AB}$旋转n°得到$\widehat{CD}$,则$\widehat{CD}$的度数是20度.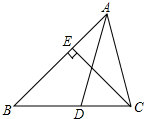 如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.
如图,AD是△ABC的角平分线,CE是△ABC的高,∠BAC=64°,∠BCE=40°,求∠ADC的度数.