题目内容
12.已知不等式组:$\left\{\begin{array}{l}{x>-1}\\{x<1}\\{x<1-k}\end{array}\right.$(1)若k=$\frac{1}{2}$时,不等式组的解集是-1<x<$\frac{1}{2}$;若k=3时,不等式组的解集是无解;
(2)若要使不等式组一定有解,则k的取值范围是k<2.
分析 (1)利用大小小大中间找;大大小小找不到确定不等式组的解集;
(2)利用大小小大中间找得到1-k>1,然后解关于k的不等式.
解答 解:(1)当k=$\frac{1}{2}$,$\left\{\begin{array}{l}{x>-1}\\{x<1}\\{x<\frac{1}{2}}\end{array}\right.$,所以不等式组的解集为-1<x<$\frac{1}{2}$;
当k=3,$\left\{\begin{array}{l}{x>-1}\\{x<1}\\{x<-2}\end{array}\right.$,所以不等式组无解;
(2)当不等式组一定有解,1-k>1,解得k<2,
所以k的取值范围为k<2.
故答案为-1<x<$\frac{1}{2}$;无解;k<2.
点评 本题考查了解一元一次不等式组:解一元一次不等式组时,一般先求出其中各不等式的解集,再求出这些解集的公共部分,利用数轴可以直观地表示不等式组的解集.解集的规律:同大取大;同小取小;大小小大中间找;大大小小找不到.

练习册系列答案
相关题目
17. 如图,在⊙O中,∠BOC=100°,则∠A等于( )
如图,在⊙O中,∠BOC=100°,则∠A等于( )
 如图,在⊙O中,∠BOC=100°,则∠A等于( )
如图,在⊙O中,∠BOC=100°,则∠A等于( )| A. | 25° | B. | 40° | C. | 50° | D. | 100° |
4.下列计算正确的是( )
| A. | $\sqrt{4}$=±2 | B. | $\sqrt{(-2)^{2}}$=-2 | C. | -$\sqrt{(-2)^{2}}$=2 | D. | $\root{3}{-8}$=-2 |

 将5个大小相同的圆板如图放置,要求一刀切下,将5个圆切成面积相等两部分,应如何切?
将5个大小相同的圆板如图放置,要求一刀切下,将5个圆切成面积相等两部分,应如何切?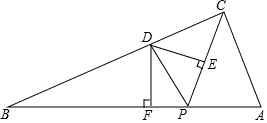 如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.
如图,在Rt△ABC中,∠ACB=90°,AC=5,BC=10,点P是边AB上任意一点,连接PC,∠CPB的平分线交BC于点D,过点D分别作PC、PB的垂线,垂足分别为点E、F,当△CED与△BDF相似时,AP的长为$\frac{5\sqrt{5}}{2}$或$\sqrt{5}$.